Chapter 1: Introduction
1.2 对称加密Setting
- Kerckhoffs’ principle:要求加密算法的安全性只依赖于密钥的安全性,而加解密算法都应当可以公开
1.3 古典加密算法
- 恺撒加密、移位加密、单字母替换、多字母移位
- 密钥空间充分性原则:任何安全的加密方案必须拥有一个能够抵御穷举搜索的密钥空间
1.4 现代密码学原则
原则1 Formal Defination
-
安全性定义包含:
-
security guarantee
regardless of any information an attacker already has, a ciphertext should leak no additional information about the underlying plaintext
-
threat model 敌手的目标是要解密密文,得到明文
- Ciphertext-only attack 唯密文攻击:敌手只能得到密文【被动攻击】
- Known-plaintext attack 已知明文攻击:敌手能获得一个或多个明文-密文对【被动攻击】
- Chosen-plaintext attack 选择明文攻击:敌手可以选择明文,并获得加密后的密文【主动攻击】
- Chosen-ciphertext attack 选择密文攻击:敌手可以选择密文,并获得解密后的明文【主动攻击】
-
原则2 Precise Assumption
原则3 Proofs of Security
Chapter 2: Perfectly Secret Encryption
2.1 符号定义
- 加密方案的元素:
- $\mathcal{M}$ ——有限消息空间,$|\mathcal{M}|>1$
- 令 $M$ 是一个随机的消息 ,对于任意 $m\in\mathcal{M}$ ,$Pr[M=m]$ 表示 $M$ 与 $m$ 一致的概率
- $\mathcal{K}$ ——有限密钥空间
- 令 $K$ 是 $\mathsf{Gen}$ 随机生成的密钥,对于任意 $k\in\mathcal{K}$ ,$Pr[K=k]$ 表示 $\mathsf{Gen}$ 生成的密钥为 $k$ 的概率
- 注:$K$ 和 $M$ 是独立的
- $\mathcal{C}$ ——密文空间
- 令 $C$ 是一个随机变量,对于任意 $c\in\mathcal{C}$ ,$Pr[C=c]$ 表示 $\mathsf{Enc}$ 加密得到的密文为 $c$ 的概率
- 给定 $\mathsf{Enc}$ ,$\mathcal{C}$ 的分布完全取决于 $\mathcal{M}$ 和 $\mathcal{K}$ 的分布
- $\mathcal{M}$ ——有限消息空间,$|\mathcal{M}|>1$
- 加密方案包含三个算法:
- $\mathsf{Gen}$ ——密钥生成
- 密钥生成算法从 $\mathcal{K}$ 中均匀地选择一个密钥 $k$
- $\mathsf{Enc}$ ——加密
- 输入 $k\in\mathcal{K}, m\in\mathcal{M}$ ,输出密文 $c\in\mathcal{C}$
- 对于概率性加密算法,记作 $c\leftarrow \mathsf{Enc}_{k}(m)$
- 对于确定性加密算法,记作 $c:=\mathsf{Enc}_{k}(m)$
- 输入 $k\in\mathcal{K}, m\in\mathcal{M}$ ,输出密文 $c\in\mathcal{C}$
- $\mathsf{Dec}$ ——解密
- 输入 $k\in\mathcal{K},c\in\mathcal{C}$ ,输出消息 $m\in\mathcal{M}$
- 一般假设解密算法是确定性的,记作 $m:=\mathsf{Dec}_{k}©$
- 输入 $k\in\mathcal{K},c\in\mathcal{C}$ ,输出消息 $m\in\mathcal{M}$
- $\mathsf{Gen}$ ——密钥生成
- Perfect Secrecy
- 定义2.3:加密方案 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是perfectly secret,如果对 $\mathcal{M}$ 上任意概率分布,任意明文 $m\in\mathcal{M}$ ,任意密文 $c\in\mathcal{C}$ 且 $Pr[C=c]>0$ 有:$Pr[M=m|C=c]=Pr[M=m]$
- 等价定义:$Pr[C=c|M=m]=Pr[C=c]$
- 引理2.4:加密方案 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是perfectly secret,当且仅当对所有 $m, m’\in\mathcal{M}$ 和所有 $c\in\mathcal{C}$ 有:$Pr[\mathsf{Enc}{k}(m)=c]=Pr[\mathsf{Enc}{k}(m’)=c]$
- 说明密文不包含任何关于明文的信息,且不可能区分加密后的 $m$ 和 $m’$
- 定义2.3:加密方案 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是perfectly secret,如果对 $\mathcal{M}$ 上任意概率分布,任意明文 $m\in\mathcal{M}$ ,任意密文 $c\in\mathcal{C}$ 且 $Pr[C=c]>0$ 有:$Pr[M=m|C=c]=Pr[M=m]$
- Perfect (adversarial) indistinguishability
- 定义敌手不可区分实验 $\mathsf{PrivK}^{eav}_{\mathcal{A},\Pi}$ (其中 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ ):
- 敌手 $\mathcal{A}$ 输出一对消息 $m_0,m_1\in\mathcal{M}$
- 选择一个比特 $b\in{0,1}$ ,计算 $c\leftarrow \mathsf{Enc}_k(m_b)$ 并发送给 $\mathcal{A}$ 。称 $c$ 为挑战密文
- $\mathcal{A}$ 输出一个比特 $b’$
- 若 $b=b’$ 则实验输出1,记作 $\mathsf{PrivK}^{eav}_{\mathcal{A},\Pi}=1$ ,此时 $\mathcal{A}$ 获胜;反之输出0
- 定义2.5:加密方案 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是perfectly indistinguishable,如果对所有 $\mathcal{A}$ 有: $Pr[\mathsf{PrivK}^{eav}_{\mathcal{A},\Pi}=1]=\frac{1}{2}$
- 引理2.6:加密方案 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是perfectly secret,当且仅当它是perfectly indistinguishable
- 定义敌手不可区分实验 $\mathsf{PrivK}^{eav}_{\mathcal{A},\Pi}$ (其中 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ ):
2.2 一次一密
- 定义:取定整数 $l>0$ , $\mathcal{M},\mathcal{C},\mathcal{K}$ 都是长度为 $l$ 的二进制串,即 ${0,1}^l$
- $\mathsf{Gen}$ :根据均匀分布从 $\mathcal{K}={0,1}^l$ 中选择一个密钥
- $\mathsf{Enc}$ :给定密钥 $k\in{0,1}^l$ 和消息 $m\in{0,1}^l$ ,输出密文 $c:=k\oplus m$
- $\mathsf{Dec}$ :给定密钥 $k\in{0,1}^l$ 和密文 $c\in{0,1}^l$ ,输出消息 $m:=k\oplus c$
- 定理2.9:一次一密方案是perfectly secret
- 局限性:
- 密钥必须和消息等长
- 只有每次加密使用不同的密钥才安全
2.3 Perfect Secrecy的局限性
- 定理2.10: $(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是perfectly secret加密方案,则 $|\mathcal{K}|>|\mathcal{M}|$ 【反证】
- Perfectly secret的加密方案中密钥空间必须大于消息空间
2.4 香农定理
- 定理2.11(香农定理):对于 $|\mathcal{M}|=|\mathcal{K}|=|\mathcal{C}|$ 的加密方案 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是perfectly secret,当且仅当:
- 每个密钥 $k\in\mathcal{K}$ 被 $\mathsf{Gen}$ 选择的概率为 $1/|\mathcal{K}|$
- 对每个 $m\in\mathcal{M}$ 和 $c\in\mathcal{C}$ ,存在唯一的密钥 $k\in\mathcal{K}$ 使得 $\mathsf{Enc}_k(m)$ 输出 $c$
Chapter 3: Private-Key Encryption
3.1 计算安全
- 放松perfect secrecy的限制:
- 仅对可行时间内的敌手保证安全(敌手可能在足够多的时间内可以破解)
- 敌手有很小的概率破解
形式化定义
- 具体定义
- 一个方案是 $(t,\varepsilon)$-安全 的,如果任何敌手在时间 $t$ 内破解该方案的概率最大为 $\varepsilon$
- 渐进定义
- 诚实各方使用一个共享的安全参数 $n$ (或记为 $1^n$ ) 来初始化加密方案,从而敌手的攻击时间和攻击成功的概率都是 $n$ 的函数:
- 敌手攻击时间:多项式时间,即存在多项式 $p$ ,对所有输入 $x\in{0,1}^*$ ,算法最多执行 $p(|x|)$ 步
- 敌手的攻击成功概率可忽略
- 定义3.4:从自然数映射到非负实数的函数 $f$ 是可忽略(negligible)的,如果对所有正多项式 $p$ ,存在 $N$ ,使得对所有 $n>N$ ,有 $f(n)<\frac{1}{p(n)}$ 【将任意可忽略函数记作 $\mathsf{negl}$】
- 命题3.6:令 $\mathsf{negl_1}$ 和 $\mathsf{negl_2}$ 为可忽略函数,则
- $\mathsf{negl_3}(n)=\mathsf{negl_1}(n)+\mathsf{negl_2}(n)$ 是可忽略的
- 对任意正多项式 $p$ ,$\mathsf{negl_4}(n)=p(n)\cdot \mathsf{negl_1}(n)$ 是可忽略的
- 一个方案是安全的,如果任何PPT (probabilistic polynomial-time概率多项式时间) 敌手破解该方案的概率可忽略
- 诚实各方使用一个共享的安全参数 $n$ (或记为 $1^n$ ) 来初始化加密方案,从而敌手的攻击时间和攻击成功的概率都是 $n$ 的函数:
3.2 定义计算安全的加密
- 定义3.7:一个对称加密方案是一个PPT算法元组 $(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ ,满足:
- $\mathsf{Gen}$ 的输入为 $1^n$ ,输出密钥 $k$ ,记作 $k\leftarrow \mathsf{Gen}(1^n)$ ,并假设任何 $k$ 满足 $|k|>n$
- $\mathsf{Enc}$ 的输入为 $k$ 和 $m\in{0,1}^*$ ,输出密文 $c$ ,记作 $c\leftarrow \mathsf{Enc}_k(m)$
- $\mathsf{Dec}$ 的输入为 $k$ 和 $c$ ,输出消息 $m$ 或错误 $\bot$ (当输入为无效密文),记作 $m:=\mathsf{Dec}_k©$
- 算法满足 $\mathsf{Dec}_k(\mathsf{Enc}_k(m))=m$
安全的基本定义
- 关于敌手能力的假设:
- 仅窃听信道(唯密文攻击)
- 多项式时间
- 定义敌手不可区分实验 $\mathsf{PrivK}^\mathsf{eav}_{\mathcal{A},\Pi}(n)$ (其中 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ ):
- 敌手 $\mathcal{A}$ 根据输入 $1^n$ 输出一对消息 $m_0,m_1$ ,且 $|m_0|=|m_1|$
- 计算 $k\leftarrow \mathsf{Gen}(1^n)$ ,选择一个比特 $b\in{0,1}$ ,计算 $c\leftarrow \mathsf{Enc}_k(m_b)$ 并发送给 $\mathcal{A}$ 。称 $c$ 为挑战密文
- $\mathcal{A}$ 输出一个比特 $b’$
- 若 $b=b’$ 则实验输出1,记作 $\mathsf{PrivK}^\mathsf{eav}_{\mathcal{A},\Pi}(n)=1$ ,此时 $\mathcal{A}$ 获胜;反之输出0
- 定义3.8(3.9):对称加密方案 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是EAV-安全的(对窃听敌手不可区分),如果对所有PPT敌手 $\mathcal{A}$ 有一个可忽略函数 $\mathsf{negl}$ ,使得对所有n:
- $Pr[\mathsf{PrivK}^\mathsf{eav}_{\mathcal{A},\Pi}(n)=1]\leq \frac{1}{2}+\mathsf{negl}(n)$
- 该式说明 $\mathcal{A}$ 正确判断加密的消息是 $m_0$ 还是 $m_1$ 的概率小于等于 $\frac{1}{2}+\mathsf{negl}(n)$
- $Pr[out_{\mathcal{A}}(\mathsf{PrivK}\mathsf{eav}_{\mathcal{A},\Pi}(n,0))=1]-Pr[out_{\mathcal{A}}(\mathsf{PrivK}\mathsf{eav}_{\mathcal{A},\Pi}(n,1))=1]\leq \mathsf{negl}(n)$
- 其中 $\mathsf{PrivK}^\mathsf{eav}{\mathcal{A},\Pi}(n,b)$ 表示实验选择了 $m_b$ 进行加密; $out{\mathcal{A}}(\mathsf{PrivK}^\mathsf{eav}_{\mathcal{A},\Pi}(n,b))$ 表示 $\mathcal{A}$ 在实验中的输出,即 $b’$
- 该式说明 $\mathcal{A}$ 不能判断进行的实验是 $\mathsf{PrivK}^\mathsf{eav}{\mathcal{A},\Pi}(n,0)$ 还是 $\mathsf{PrivK}^\mathsf{eav}{\mathcal{A},\Pi}(n,1)$
- $Pr[\mathsf{PrivK}^\mathsf{eav}_{\mathcal{A},\Pi}(n)=1]\leq \frac{1}{2}+\mathsf{negl}(n)$
语义安全
- 不可区分意味着密文不会泄露任何一比特的明文
- 定理3.10: $\Pi=(\mathsf{Enc},\mathsf{Dec})$ 是一个对长度为 $l$ 的消息的对称加密方案,并且是EAV-安全的。则对所有PPT敌手 $\mathcal{A}$ 和任何 $i\in{1,…,l}$ ,存在一个可忽略函数 $\mathsf{negl}$ 使得:【其中 $m^i$ 表示消息的第 $i$ 比特;$\mathcal{A}(1^n,\mathsf{Enc}_k(m))$ 表示 $\mathcal{A}$ 收到挑战密文后的输出 $b’$ 】
$$Pr[\mathcal{A}(1n,\mathsf{Enc}_k(m))=mi]\leq\frac{1}{2}+\mathsf{negl}(n)$$
- 定理3.10: $\Pi=(\mathsf{Enc},\mathsf{Dec})$ 是一个对长度为 $l$ 的消息的对称加密方案,并且是EAV-安全的。则对所有PPT敌手 $\mathcal{A}$ 和任何 $i\in{1,…,l}$ ,存在一个可忽略函数 $\mathsf{negl}$ 使得:【其中 $m^i$ 表示消息的第 $i$ 比特;$\mathcal{A}(1^n,\mathsf{Enc}_k(m))$ 表示 $\mathcal{A}$ 收到挑战密文后的输出 $b’$ 】
- 不可区分意味着没有敌手能从密文中学习到任何明文的函数
- 定理3.11:$\Pi=(\mathsf{Enc},\mathsf{Dec})$ 是一个对长度为 $l$ 的消息的对称加密方案,并且是EAV-安全的。则对所有PPT敌手 $\mathcal{A}$ 存在一个PPT算法 $\mathcal{A’}$ ,使得对任何 $S\subseteq {0,1}^l$ 和任何函数 $f: {0,1}^l\rightarrow{0,1}$ ,存在一个可忽略函数 $negl$ 使得:
$$
|Pr[\mathcal{A}(1n,\mathsf{Enc}_k(m))=f(m)]-Pr[\mathcal{A’}(1n)=f(m)]|\leq \mathsf{negl}(n)
$$
- 定理3.11:$\Pi=(\mathsf{Enc},\mathsf{Dec})$ 是一个对长度为 $l$ 的消息的对称加密方案,并且是EAV-安全的。则对所有PPT敌手 $\mathcal{A}$ 存在一个PPT算法 $\mathcal{A’}$ ,使得对任何 $S\subseteq {0,1}^l$ 和任何函数 $f: {0,1}^l\rightarrow{0,1}$ ,存在一个可忽略函数 $negl$ 使得:
3.3 构建安全加密方案
伪随机生成器
伪随机生成器 $G$ 是一个高效、确定性的算法,用于将一个短的、均匀的字符串 (seed) 转变为一个长的、伪随机的字符串
- 定义3.14:令 $l$ 为一个多项式,$G$ 为一个确定性多项式时间算法,使得对任何 $n$ 和输入 $s\in{0,1}^n$ ,输出 $G(s)$ 是一个长度为 $l(n)$ 的字符串。称 $G$ 是一个伪随机生成器,如果满足:
- 扩展性:对任意 $n$ 满足 $l(n)>n$
- 伪随机性:对任意PPT算法 $D$ ,存在一个可忽略函数使得:【其中 $r\in {0,1}^{l(n)}$】
$$
|Pr[D(G(s))=1]-Pr[D®=1]|\leq \mathsf{negl}(n)
$$
- 称 $l$ 为 $G$ 的扩展系数
- 之所以生成的字符串是伪随机而不是均匀的,举例说明:$l(n)=2n$ 时,长度为 $2n$ 的字符串空间为 $2^{2n}$ ,选择任意一个 $r\in {0,1}^{2n}$ 的概率为 $1/2^{2n}$ ,是均匀的;但是由于 $s$ 的长度为 $n$ ,所以 $G(s)$ 的字符串空间为 $2^n$ ,选择到的概率为 $1/2^n$ ,不是均匀的
流密码
流密码是一对确定性算法 $(\mathsf{Init}, \mathsf{GetBits})$
- $\mathsf{Init}$ 输入seed $s$ 和可选的初始化向量 $IV$ ,输出初始状态 $st_0$
- $\mathsf{GetBits}$ 输入状态信息 $st_i$ ,输出一个比特 $y$ 并更新状态到 $st_{i+1}$
算法3.16:

规约证明
将证明一个敌手 $\mathcal{A}$ 成功破解一个方案 转换为 证明一个算法 $\mathcal{A’}$ 解决一个难题,具体步骤如下:
- 选定一个敌手 $\mathcal{A}$ 攻击 $\Pi$ ,攻击成功的概率为 $\varepsilon(n)$ ;
- 构建一个算法 $\mathcal{A’}$ ,它使用敌手 $\mathcal{A}$ 作为子程序来尝试解决问题 $X$ 。注意: $\mathcal{A’}$ 不知道 $\mathcal{A}$ 是如何工作的,它只知道 $\mathcal{A}$ 要攻击 $\Pi$ 。当输入一个问题 $X$ 的实例 $x$ 时, $\mathcal{A’}$ 为 $\mathcal{A}$ 模拟一个 $\Pi$ 的实例,使得:
- $\mathcal{A}$ 无法区分自己是作为 $\mathcal{A’}$ 的子程序在运行还是其本身在攻击 $\Pi$ ;
- 如果 $\mathcal{A}$ 成功破解 $\mathcal{A’}$ 模拟的 $\Pi$ ,则 $\mathcal{A’}$ 能解决问题 $x$ ,其概率至少为 $1/p(n)$ ;
- 根据上一点, $\mathcal{A’}$ 解决 $X$ 的概率为 $\varepsilon(n)/p(n)$ 。若 $\varepsilon(n)$ 不是可忽略的,则 $\varepsilon(n)/p(n)$ 也不是可忽略的,从而得到一个算法 $\mathcal{A’}$ 以不可忽略的概率解决 $X$ ,与假设( $X$ 是一个计算难题,无法在多项式时间内解决)矛盾;
- 综上,如果 $X$ 确实是计算难题,则没有 $\mathcal{A}$ 能以不可忽略的概率破解 $\Pi$ 。换言之, $\Pi$ 是计算安全的。
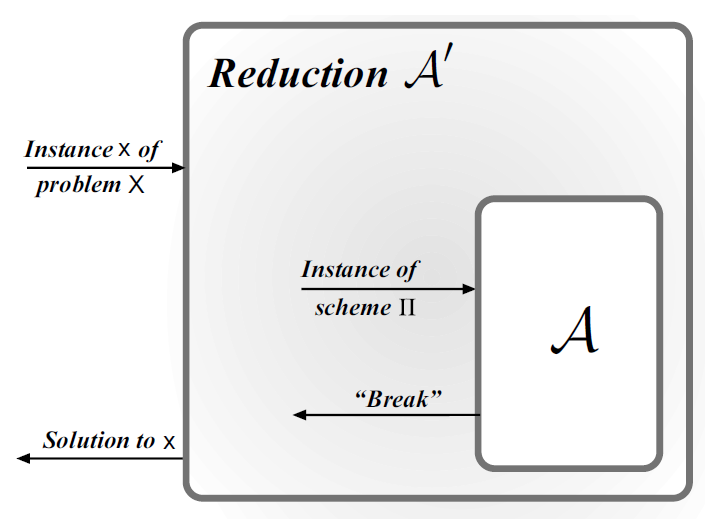
安全的定长加密方案
用生成器对密钥进行扩充,以达到一次一密的效果
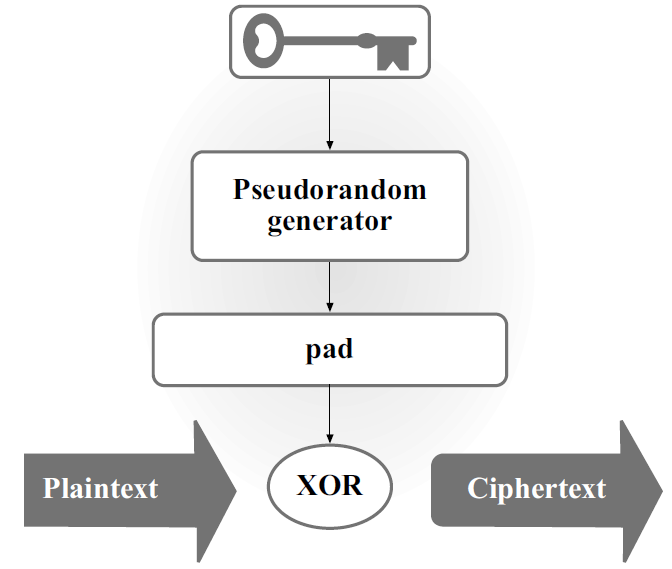
具体构造3.17如下:

- 定理3.18:如果 $G$ 是伪随机生成器,则上述构造的加密方案是EAV-安全的
规约证明3.18:
使用 $\mathcal{A}$ 来构造一个判别器 $D$ ,将 $\mathcal{A}$ 正确选择 $\Pi$ 加密的消息的能力规约到 $D$ 分辨 $G$ 的输出和均匀字符串的能力,从而由 $G$ 的安全性能推导出 $\Pi$ 的安全性。
$D$ 的构造如下,$D$ 的目标是分辨输入 $w$ 是随机串还是由伪随机生成器生成的:

定义 $\widetilde{\Pi}=(\widetilde{\mathsf{Gen}},\widetilde{\mathsf{Enc}},\widetilde{\mathsf{Dec}})$ 为一次一密方案:
- $\widetilde{\mathsf{Gen}}(1^n)$ 输出长度为 $l(n)$ 的密钥 $k$ ;
- $\widetilde{\mathsf{Enc}}$ 使用 $k$ 加密长度为 $l(n)$ 的消息:$c:=k\oplus m$ ;
根据一次一密的perfect secrecy:
$$
Pr[\mathsf{PrivK}^{eav}_{\mathcal{A},\widetilde{\Pi}}(n)=1]=\frac{1}{2} \tag{3.3}
$$
对 $D$ 进行分析:
- 若 $w$ 是从 ${0,1}^{l(n)}$ 中均匀选出的,则 $\mathcal{A}$ 作为 $D$ 的子程序运行的视图和在实验 $\mathsf{PrivK}^{eav}{\mathcal{A},\widetilde{\Pi}}(n)$ 中的视图完全一致,即:
$$
Pr{w\leftarrow {0,1}{l(n)}}[D(w)=1]=Pr[\mathsf{PrivK}{eav}_{\mathcal{A},\widetilde{\Pi}}(n)=1]=\frac{1}{2} \tag{3.4}
$$ - 若 $w$ 是通过 $w=G(k),,k\in {0,1}^n$ 生成的,则 $\mathcal{A}$ 作为 $D$ 的子程序运行的视图和在实验 $\mathsf{PrivK}^{eav}{\mathcal{A},\Pi}(n)$ 中的视图完全一致,即
$$
Pr{k\leftarrow {0,1}n}[D(G(k))=1]=Pr[\mathsf{PrivK}{eav}_{\mathcal{A},\Pi}(n)=1] \tag{3.5}
$$
由于 $G$ 是伪随机生成器,所以存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
|Pr_{w\leftarrow {0,1}^{l(n)}}[D(w)=1]-Pr_{k\leftarrow {0,1}^n}[D(G(k))=1]|\leq \mathsf{negl}(n)
$$
根据公式 $(3.4),,(3.5)$ 得:
$$
|\frac{1}{2}-Pr[\mathsf{PrivK}^{eav}_{\mathcal{A},\Pi}(n)=1]|\leq \mathsf{negl}(n)
$$
即 $Pr[\mathsf{PrivK}^{eav}_{\mathcal{A},\Pi}(n)=1]\leq \frac{1}{2}+\mathsf{negl}(n)$ ,从而方案 $\Pi$ 是EAV-安全的。
3.4 更强的安全概念
多消息加密——修改安全目标
- 多消息窃听实验 $\mathsf{PrivK}^\mathsf{mult}_{\mathcal{A},\Pi}(n)$ :
- 敌手 $\mathcal{A}$ 得到输入 $1^n$ ,并输出一对相同长度的消息列表: $\vec{M_0}=(m_{0,1},…,m_{0,t})$ 和 $\vec{M_1}=(m_{1,1},…,m_{1,t})$ ,其中 $|m_{0,i}|=|m_{1,i}|$ ;
- $k\leftarrow \mathsf{Gen(1^n)}$ ,并随机选择 $b\in{0,1}$ 。对所有 $i$ ,计算 $c_i\leftarrow \mathsf{Enc}k(m{b,i})$ ,将 $\vec{C}=(c_1,…,c_t)$ 发送给 $\mathcal{A}$ ;
- $\mathcal{A}$ 输出一比特 $b’$ ;
- 若 $b=b’$ 则实验输出1,$\mathcal{A}$ 获胜,反之输出0。
- 定义3.19:一个对称加密方案 $\Pi=(\mathsf{Gen,Enc,Dec})$ 是多消息EAV-安全的,如果对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{PrivK}^\mathsf{mult}_{\mathcal{A},\Pi}(n)=1]\leq\frac{1}{2}+\mathsf{negl}(n)
$$ - 命题3.20:存在一个对称加密算法是EAV-安全的,但不是多消息EAV-安全的。【eg. 一次一密】
- 定理3.21:如果 $\Pi$ 是一个无状态的加密方案且 $\mathsf{Enc}$ 是确定性算法,则 $\Pi$ 不可能是多消息EAV-安全的。
CPA-安全(选择明文攻击)——增强威胁模型
- CPA不可区分实验 $\mathsf{PrivK}^\mathsf{cpa}_{\mathcal{A},\Pi}(n)$ :
- $k\leftarrow \mathsf{Gen(1^n)}$ ;
- 敌手 $\mathcal{A}$ 得到输入 $1^n$ 并能够使用oracle $\mathsf{Enc}_k(\cdot)$,输出一对相同长度的消息 $m_0$ 和 $m_1$ ;
- 随机选择 $b\in{0,1}$ ,计算 $c\leftarrow \mathsf{Enc}k(m{b})$ ,并发送给 $\mathcal{A}$ ;
- $\mathcal{A}$ 输出一比特 $b’$ ;
- 若 $b=b’$ 则实验输出1,$\mathcal{A}$ 获胜,反之输出0。
- 定义3.22:对称加密方案 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是CPA-安全的(对选择明文攻击不可区分),如果对所有PPT敌手 $\mathcal{A}$ 有一个可忽略函数 $\mathsf{negl}$ ,使得对所有n:
$$Pr[\mathsf{PrivK}^\mathsf{cpa}_{\mathcal{A},\Pi}(n)=1]\leq \frac{1}{2}+\mathsf{negl}(n)$$
多消息加密的CPA-安全
- 定义oracle $\mathsf{LR}_{k,b}(\cdot,\cdot)$ :输入两个等长的消息 $m_0$ ,$m_1$ ,若 $b=0$ 输出 $c\leftarrow \mathsf{Enc}_k(m_0)$ ;若 $b=1$ 输出 $c\leftarrow \mathsf{Enc}_k(m_1)$
- LR-oracle实验 $\mathsf{PrivK}^\mathsf{LR-cpa}_{\mathcal{A},\Pi}(n)$ :
- $k\leftarrow \mathsf{Gen(1^n)}$ ;
- 随机选择 $b\in{0,1}$ ;
- 敌手 $\mathcal{A}$ 得到输入 $1^n$ 并能够使用oracle $\mathsf{LR}{k,b}(\cdot,\cdot)$ 【 $\mathcal{A}$ 能通过请求 $\mathsf{LR}{k,b}(m_{0,1},m_{1,1})$,…,$\mathsf{LR}{k,b}(m{0,t},m_{1,t})$ 来获取消息列表的加密结果,同时也可以通过请求 $\mathsf{LR}_{k,b}(m,m)$ 来获得 $\mathsf{Enc}_k(m)$ 】,输出一对相同长度的消息 $m_0$ 和 $m_1$ ;
- 计算 $c\leftarrow \mathsf{Enc}k(m{b})$ ,并发送给 $\mathcal{A}$ ;
- $\mathcal{A}$ 输出一比特 $b’$ ;
- 若 $b=b’$ 则实验输出1,$\mathcal{A}$ 获胜,反之输出0。
- 定义3.23:对称加密方案 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是多消息CPA-安全的,如果对所有PPT敌手 $\mathcal{A}$ 有一个可忽略函数 $\mathsf{negl}$ ,使得对所有n:
$$Pr[\mathsf{PrivK}^\mathsf{LR-cpa}_{\mathcal{A},\Pi}(n)=1]\leq \frac{1}{2}+\mathsf{negl}(n)$$ - 定理3.24:任何CPA-安全的对称加密方案都是多消息CPA-安全的
3.5 构造CPA-安全的加密方案
伪随机函数
- 定义keyed函数 $F(k,x):{0,1}^\times {0,1}^\rightarrow {0,1}^$ ,一般而言可以固定密钥 $k$ ,记作 $F_k(x)=F(k,x)$ ,而 $F_k(x):{0,1}^\rightarrow {0,1}^*$ 。安全参数 $n$ 规定了密钥、输入、输出的长度,从而 $F_k(x)$ 是条件 $k\in{0,1}^n$ 下的一个将长度为 $n$ 的输入映射到长度为 $n$ 的输出的函数。
- 称函数 $F$ 是伪随机的,如果 $F_k(x)$ 与 $f:{0,1}^n\rightarrow {0,1}^n$ 不可区分【所有 $f$ 的集合记作 $\mathsf{Func}_n$】
- 可以将 $f$ 看作一个表,根据长度 $n$ 的输入查表得到长度 $n$ 的输出,输入可以固定顺序为 $0^n$ 到 $1^n$ ,则该表有 $2^n$ 行,每个输入对应的输出长度为 $n$ ,即每行长度为 $n$ ,因此函数 $f$ 可以看作一个长度为 $2^n\cdot n$ 的序列,从而 $f$ 的取值空间大小为 $2{2n\cdot n}$ 【$F_k$ 的取值空间为 $2^n$】
- 称函数 $F$ 是伪随机的,如果 $F_k(x)$ 与 $f:{0,1}^n\rightarrow {0,1}^n$ 不可区分【所有 $f$ 的集合记作 $\mathsf{Func}_n$】
- 定义3.25:令 $F:{0,1}^\times {0,1}^\rightarrow {0,1}^*$ 为一个keyed函数。$F$ 是一个伪随机函数,如果对所有PPT判别器 $D$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
|Pr[D{F_k(\cdot)}(1n)=1]-Pr[D{f(\cdot)}(1n)=1]|\leq\mathsf{negl}(n)
$$- 注:$D$ 并不知道具体的 $k$
伪随机排列
- 令 $\mathsf{Perm}_n$ 是 ${0,1}^n$ 的全排列,大小为 $(2^n)!$
- 若函数 $f\in\mathsf{Perm}_n$ ,说明不同输入映射到的输出是不同的
- $F$ 是一个keyed排列,如果 $F_k$ 的值是全排列; $F$ 是efficient的,如果可以在多项式时间内计算 $F_k(x)$ 和 $F_k^{-1}(y)$
- $F$ 是伪随机排列,如果 $F_k(x)$ 与 $f\in\mathsf{Perm}_n$ 不可区分
- 命题3.27:如果 $F$ 是一个伪随机排列且 $l_{in}(n)\geq n$ ,则 $F$ 也是一个伪随机函数
- 定义3.28:令 $F:{0,1}^\times {0,1}^\rightarrow {0,1}^*$ 为一个keyed排列。$F$ 是一个强伪随机排列,如果对所有PPT判别器 $D$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
|Pr[D{F_k(\cdot),F_k{-1}(\cdot)}(1n)=1]-Pr[D{f(\cdot),f{-1}(\cdot)}(1n)=1]|\leq\mathsf{negl}(n)
$$
伪随机函数与伪随机生成器的关系
- 伪随机生成器 $G$ 可以由伪随机函数 $F$ 得到:$G(s)=F_s(1)||F_s(2)||…||F_s(l)$
- 根据伪随机函数构造流密码3.29:

伪随机函数构造的CPA-安全加密
- 证明基于伪随机函数的构造的安全性:首先假设构造中的伪随机函数被以一个随机函数替换,再通过规约证明来说明这个改变不会影响敌手成功的概率,最后再证明修改后的构造是安全的
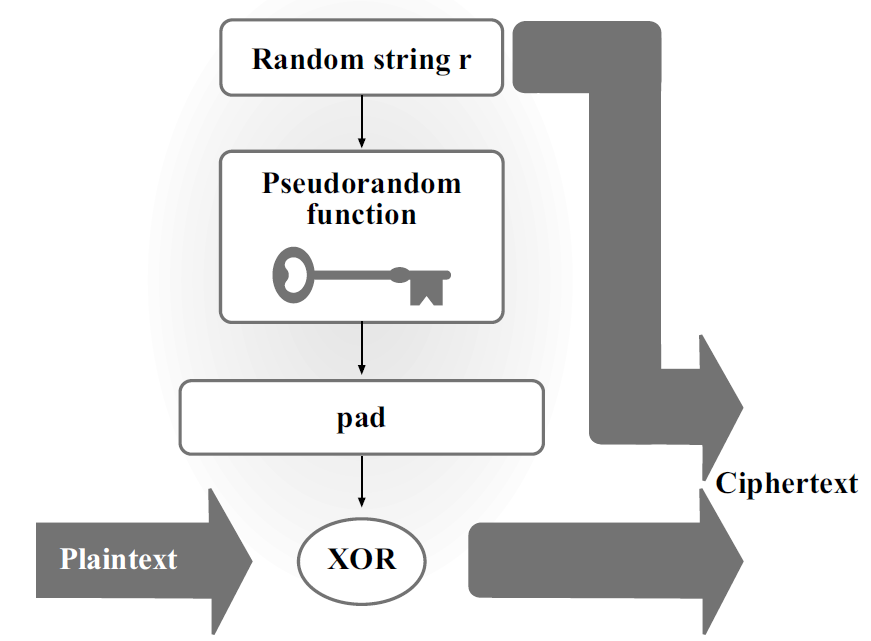
- 构造3.30:
- 缺点在于生成的密文长度是明文的两倍

- 定理3.31:如果 $F$ 是一个伪随机函数,则上述构造是CPA-安全的【证明on P83】
3.6 工作模式
流密码的工作模式
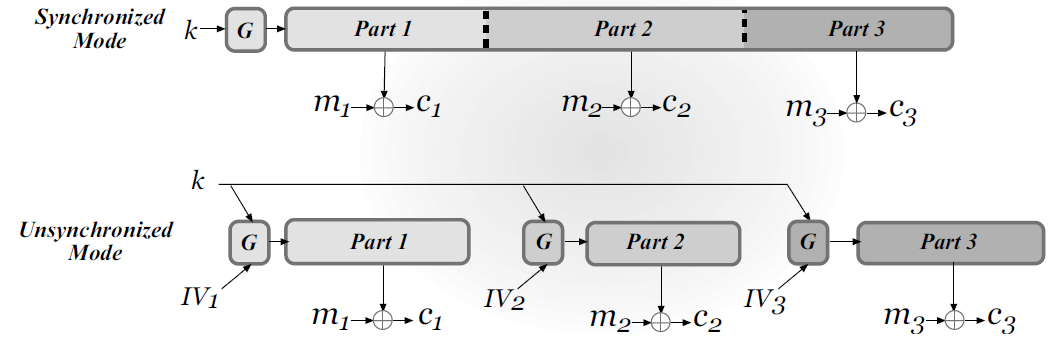
- 同步模式:有状态,需要通信双方同步,基于算法3.16和构造3.17
- 令发送方为A,接收方为B,双方计算 $\mathsf{st}_0:=\mathsf{Init}(k)$
- 发送第一条长度为 $l_1$ 的消息 $m_1$ ,A根据 $\mathsf{st}0$ 运行 $l_1$ 次 $\mathsf{GetBits}$ ,得到 $\mathsf{pad}1\overset{def}{=}y_1,…,y{l_1}$ 并更新状态到 $\mathsf{st}{l_1}$ ,然后发送 $c_1:=\mathsf{pad}_1 \oplus m_1$ ;而B解密通过 $m_1:=\mathsf{pad}_1 \oplus c_1$
- 发送第二条长度为 $l_2$ 的消息 $m_2$ ,A根据 $\mathsf{st}{l_1}$ 运行 $l_2$ 次 $\mathsf{GetBits}$ ,得到 $\mathsf{pad}2\overset{def}{=}y{l_1+1},…,y{l_1+l_2}$ 并更新状态到 $\mathsf{st}_{l_1+l_2}$ ,然后发送 $c_2:=\mathsf{pad}_2 \oplus m_2$ ;而B解密通过 $m_2:=\mathsf{pad}_2 \oplus c_2$ ,以此类推
- 自同步模式:无状态CPA-安全,基于构造3.30,其中的 $F_k(IV)\overset{def}{=}G_\infty(k,IV,1^l)$
分组密码的工作模式
使用分组密码构造CPA-安全的加密方案,改进构造3.30,使得密文长度减小。令 $F$ 为分组长度为 $n$ 的分组密码,需要加密的消息记为 $m=m_1,m_2,…,m_l$ 且 $m_i\in{0,1}^n$
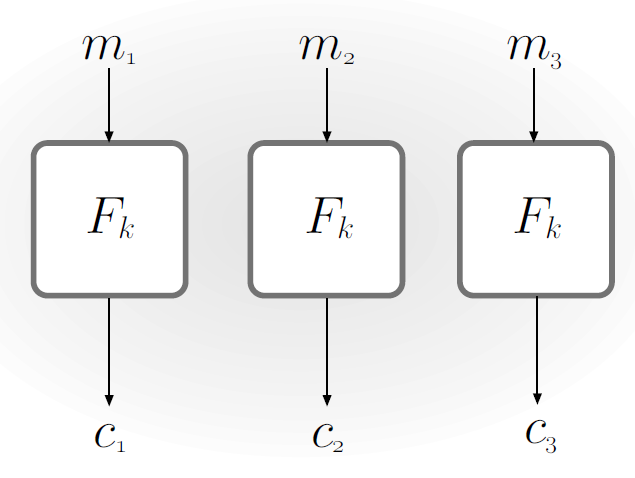
- ECB模式(Electronic Code Book):$c:=\langle F_k(m_1),…,F_k(m_l)\rangle$ ,它是确定性算法,因此不是CPA-安全的,同时它也不是EAV-安全的,因为每一个分组的block都相同
-
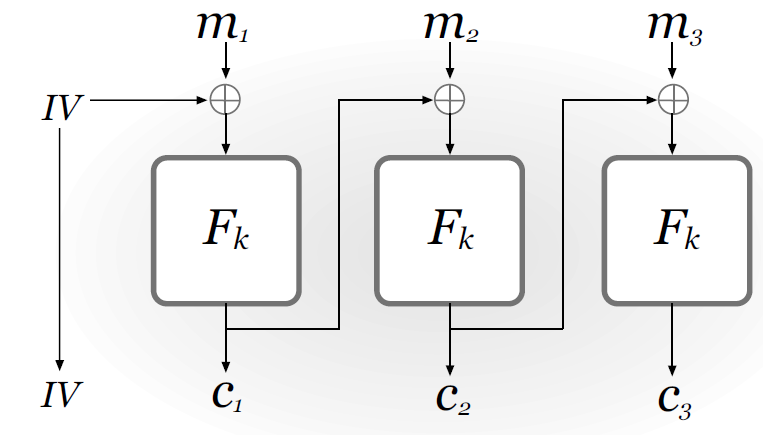
CBC模式(Cipher Block Chaining):概率性算法,若 $F$ 是一个伪随机排列,则CBC-模式加密是CPA-安全的
-
缺点:加解密只能串行,不能并行,因为后面的block依赖于前面block的输出
-
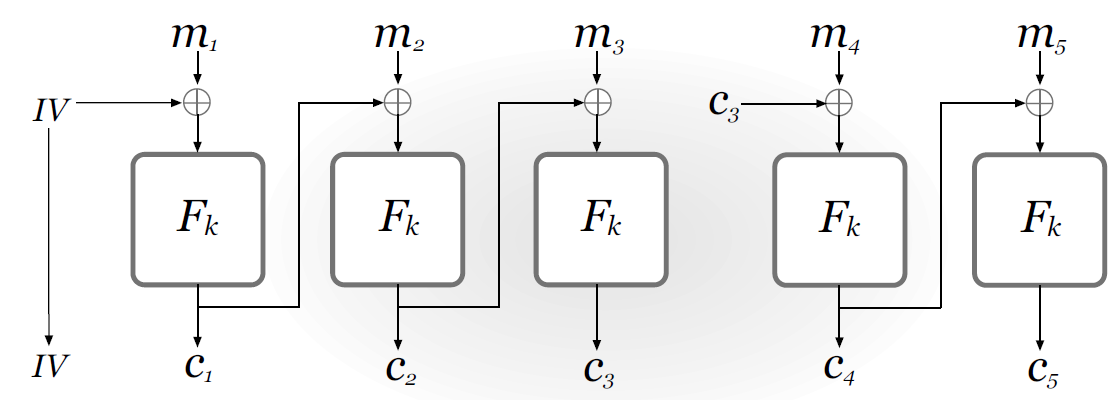
链式CBC:对一种选择明文攻击不安全,构造攻击如下:
-
假设敌手知道 $m_1\in{m_10,m_11}$ ,并且得到了密文 $IV,c_1,c_2,c_3$ ,接着构造 $m_4=IV\oplus m_1^0\oplus c_3$ ,得到输出 $c_4$ 。从而可以得出 $m_1=m_1^0$ 当且仅当 $c_4=c_1$ ,因此敌手可以从 ${m_10,m_11}$ 中选出正确的 $m_1$
-
-
-
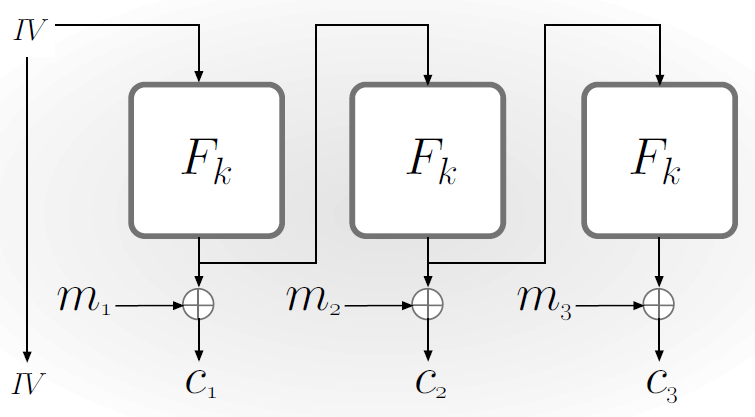
OFB模式(Output Feedback):可以看作是自同步流密码,$F$ 不需要是一个伪随机排列,消息长度不需要进行填充,且每一步的状态都是保密的。若 $F$ 是一个伪随机函数,则OFB模式是CPA-安全的。虽然加解密都只能串行执行,但是加解密用的伪随机串可以提前计算
-
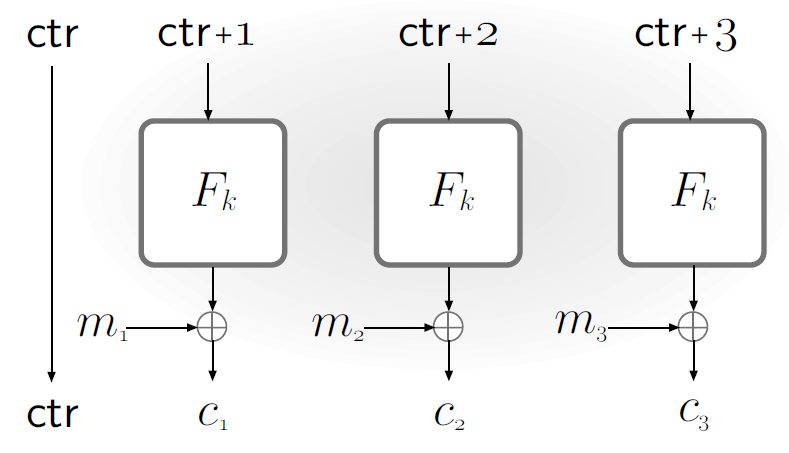
CTR模式(Counter):也可以看作自同步流密码,具体构造如下:
-
选择一个随机值 $\mathsf{ctr}\in{0,1}^n$ ,计算伪随机串 $y_i:=F_k(\mathsf{ctr}+i)$ 【其中 $\mathsf{ctr}+i$ 是整数模 $2^n$ 相加】,从而第 $i$ 个密文块为 $c_i:=y_i\oplus m_i$
-
$F$ 不需要是一个伪随机排列,消息长度不需要进行填充,且每一步的状态都是保密的,加解密可以并行执行,且伪随机串可以提前计算
-
定理3.32:若 $F$ 是一个伪随机函数,则CRT模式是CPA-安全的。【证明on P93】
-
3.7 选择密文攻击
CCA-安全
- CCA不可区分实验 $\mathsf{PrivK}^\mathsf{cca}_{\mathcal{A},\Pi}(n)$ :
- $k\leftarrow \mathsf{Gen(1^n)}$ ;
- 敌手 $\mathcal{A}$ 得到输入 $1^n$ 并能够使用oracle $\mathsf{Enc}_k(\cdot)$ 和 $\mathsf{Dec}_k(\cdot)$ ,输出一对相同长度的消息 $m_0$ 和 $m_1$ ;
- 随机选择 $b\in{0,1}$ ,计算 $c\leftarrow \mathsf{Enc}k(m{b})$ ,并发送给 $\mathcal{A}$ ;
- $\mathcal{A}$ 可以继续使用 $\mathsf{Enc}_k(\cdot)$ 和 $\mathsf{Dec}_k(\cdot)$ ,但不能对挑战密文使用 $\mathsf{Dec}_k(\cdot)$。最终 $\mathcal{A}$ 输出一比特 $b’$ ;
- 若 $b=b’$ 则实验输出1,$\mathcal{A}$ 获胜,反之输出0。
- 定义3.33:对称加密方案 $\Pi=(\mathsf{Gen}, \mathsf{Enc}, \mathsf{Dec})$ 是CCA-安全的(对选择密文攻击不可区分),如果对所有PPT敌手 $\mathcal{A}$ 有一个可忽略函数 $\mathsf{negl}$ ,使得对所有n:
$$Pr[\mathsf{PrivK}^\mathsf{cca}_{\mathcal{A},\Pi}(n)=1]\leq \frac{1}{2}+\mathsf{negl}(n)$$ - 注:任何CCA-安全的对称加密方案都是多消息CCA-安全的
- 之前所讨论的所有加密方案都不是CCA安全的,例如对于构造3.30:敌手选择 $m_0=0n,,m_1=1n$ ,在收到密文 $c=\langle r,s\rangle$ 之后,敌手反转 $s$ 的第一位,并将新的密文 $c’=\langle r,s’\rangle$ 发送到 $\mathsf{Dec}_k(\cdot)$ 进行解密,若结果是 $10^{n-1}$ 说明 $b=0$ ,若结果是 $01^{n-1}$ 说明 $b=1$
- CCA-安全的一个重要性质是non-malleability,即对于一个密文,若对其做一些修改,则解密要么无效要么结果与原本的结果毫无关系
Padding-Oracle Attacks
攻击者只需要知道修改后的密文是否能够有效解密,具体攻击方法见P98
Chapter 4: Message Authentication Codes
4.2 MAC(消息认证码)定义
- 定义4.1:一个MAC包含三个PPT算法 $(\mathsf{Gen},\mathsf{Mac},\mathsf{Vrfy})$ :满足 $\mathsf{Vrfy}_k(m,\mathsf{Mac}_k(m))=1$
- $\mathsf{Gen}$ 根据输入安全参数 $1^n$ ,输出密钥 $k,,|k|\geq n$
- $\mathsf{Mac}$ 根据输入密钥 $k$ 和消息 $m\in{0,1}^*$ ,输出一个标签 $t$ ,即 $t\leftarrow \mathsf{Mac}_k(m)$
- $\mathsf{Vrfy}$ 是确定性算法,根据输入密钥 $k$ 、消息 $m$ 和标签 $t$ ,输出一比特 $b$ ,即 $b:=\mathsf{Vrfy}_k(m,t)$ 。若 $b=1$ 说明验证通过
- 消息认证实验 $\mathsf{Mac{-}forge}_{\mathcal{A},\Pi}(n)$ :
- $k\leftarrow \mathsf{Gen}(1^n)$
- 敌手 $\mathcal{A}$ 得到输入 $1^n$ 并能够使用oracle $\mathsf{Mac}_k(\cdot)$ 。敌手最终输出 $(m,t)$ 。令 $\mathcal{Q}$ 表示 $\mathcal{A}$ 对oracle的所有请求集合
- $\mathcal{A}$ 成功当且仅当(1). $\mathsf{Vrfy}_k(m,t)=1$ 和(2). $m\notin \mathcal{Q}$ ,此时实验输出1
- 定义4.2:MAC算法 $\Pi=(\mathsf{Gen},\mathsf{Mac},\mathsf{Vrfy})$ 是安全的,若对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{Mac{-}forge}_{\mathcal{A},\Pi}(n)=1]\leq \mathsf{negl}(n)
$$- 以上定义的安全的MAC算法不能抵抗重放攻击,因为它不对消息的状态进行验证,只要 $(m,t)$ 是有效的就可以通过验证
- 消息认证增强实验 $\mathsf{Mac{-}sforge}_{\mathcal{A},\Pi}(n)$ :
- $k\leftarrow \mathsf{Gen}(1^n)$
- 敌手 $\mathcal{A}$ 得到输入 $1^n$ 并能够使用oracle $\mathsf{Mac}_k(\cdot)$ 。敌手最终输出 $(m,t)$ 。令 $\mathcal{Q}$ 表示所有的请求过的 $(m,t)$ 集合
- $\mathcal{A}$ 成功当且仅当(1). $\mathsf{Vrfy}_k(m,t)=1$ 和(2). $(m,t)\notin \mathcal{Q}$ ,此时实验输出1
- 定义4.3:MAC算法 $\Pi=(\mathsf{Gen},\mathsf{Mac},\mathsf{Vrfy})$ 是强安全的,若对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{Mac{-}sforge}_{\mathcal{A},\Pi}(n)=1]\leq \mathsf{negl}(n)
$$ - 命题4.4:令 $\Pi=(\mathsf{Gen},\mathsf{Mac},\mathsf{Vrfy})$ 是一个安全的MAC算法,则它也是强安全的
4.3 构造安全MAC
固定长度MAC
-
构造4.5:

-
定理4.6:若 $F$ 是一个伪随机函数,则构造4.5对于长度为 $n$ 的消息是安全的MAC【证明on P117】
任意长度MAC
-
构造4.7:

-
定理4.8:如果 $\Pi’$ 是安全的定长MAC,则构造4.7也是安全MAC【证明on P120】
4.4 CBC-MAC
-
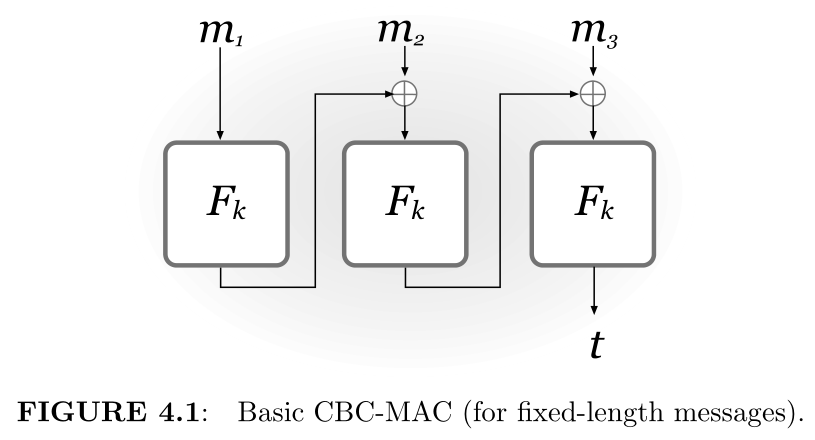
基本构造4.11(定长CBC-MAC):

-
定理4.12:令 $\ell$ 为多项式,若 $F$ 是伪随机函数,则构造4.11是对长度为 $\ell(n)\cdot n$ 的消息的安全MAC
-
构造任意长度的CBC-MAC
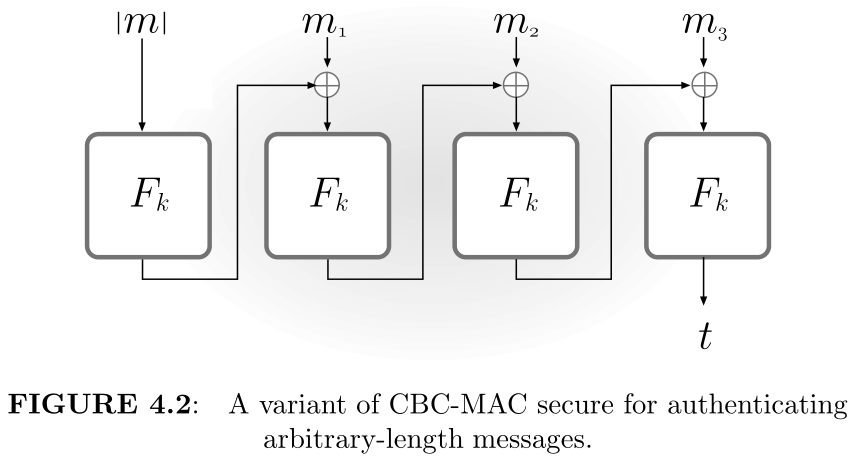
-
*安全性证明on P125,包括:
- 定理4.13
- 断言4.14
- 断言4.15
4.5 认证加密
定义
- 不可伪造加密实验 $\mathsf{Enc{-}Forge}_{\mathcal{A},\Pi}(n)$ :
- $k\leftarrow \mathsf{Gen}(1^n)$
- 敌手 $\mathcal{A}$ 得到输入 $1^n$ 并能够使用加密oracle $\mathsf{Enc}_k(\cdot)$ 。敌手最终输出密文 $c$
- 令 $m:=\mathsf{Dec}_k©$ ,令 $\mathcal{Q}$ 表示 $\mathcal{A}$ 对加密oracle的所有请求集合。实验输出1当且仅当(1) $m\neq\perp$ 和(2) $m\notin \mathcal{Q}$
- 若敌手可以伪造一个密文,使其能够成功解密,则敌手获胜
- 定义4.16:一个对称加密方案 $\Pi$ 是不可伪造的,如果对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{Enc{-}Forge}_{\mathcal{A},\Pi}(n)=1]\leq\mathsf{negl}(n)
$$ - 定义4.17:一个对称加密方案是一个认证加密方案,如果它既是CCA-安全的又是不可伪造的
一般构造
-
Encrypt-and-authenticate:
$$
c\leftarrow\mathsf{Enc}{k_E}(m),,and,,t\leftarrow\mathsf{Mac}{k_E}(m)
$$- 不能保证基本的安全性,因为MAC并没有机密性要求,从而可能泄露关于 $m$ 的信息
-
Authenticate-then-encrypt:
$$
t\leftarrow\mathsf{Mac}{k_E}(m),,and,,c\leftarrow\mathsf{Enc}{k_E}(m||t)
$$- 不能保证一定是认证加密方案,例如对于CBC模式加密,将 $t$ 看作是对消息 $m$ 的填充,则对于解密失败存在两种情况:填充错误或MAC验证失败,但只要攻击者能分辨两种错误,就可以正确解密,如3.7节最后的Padding-Oracle Attacks所示
-
Encrypt-then-authenticate:
$$
c\leftarrow\mathsf{Enc}{k_E}(m),,and,,t\leftarrow\mathsf{Mac}{k_E}©
$$-
正式构造4.18如下:

-
定理4.19:令 $\Pi_E$ 是CPA-安全的对称加密方案, $\Pi_M$ 是强安全的MAC,则构造4.18是认证加密方案【证明on P136】
-
Chapter 5: Hash Functions and Applications
5.1 定义
抗碰撞
- 定义5.1:哈希函数是一对PPT算法 $(\mathsf{Gen},H)$ ,满足:
- $\mathsf{Gen}$ 是一个概率算法,输入安全参数 $1^n$ ,输出密钥 $s$ 。假设 $1^n$ 隐含在 $s$ 中
- $H$ 根据输入密钥 $s$ 和字符串 $x\in{0,1}^*$ ,输出字符串 $Hs(x)\in{0,1}{\ell(n)}$
- collision-finding实验 $\mathsf{Hash{-}coll}_{\mathcal{A},\Pi}(n)$ :
- $s\leftarrow\mathsf{Gen}(1^n)$
- 敌手 $\mathcal{A}$ 根据输入 $s$ 输出 $x,x’$
- 实验输出1当且仅当 $x\neq x’$ 且 $Hs(x)=Hs(x’)$ ,此时称 $\mathcal{A}$ 找到了碰撞
- 定义5.2:哈希函数 $\Pi=(\mathsf{Gen},H)$ 是抗碰撞的,如果对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{Hash{-}coll}_{\mathcal{A},\Pi}(n)=1]\leq \mathsf{negl}(n)
$$ - 在实际应用中,哈希函数通常是unkeyed的,即 $H: {0,1}*\rightarrow{0,1}\ell$ ,从理论的角度这是不安全的,因为所有哈希函数在生成的时候就硬编码了碰撞对 $(x,x’)$ ,但是实践中找到这样的碰撞对是困难的,因此unkeyed哈希函数还是计算安全的
较弱的安全概念
- 弱抗碰撞性(抗第一原像):给定 $s,x$ ,PPT敌手找到 $x’\neq x$ 使得 $Hs(x’)=Hs(x)$ 是不可行的
- 单向性(抗第二原像):给定 $s,y$ ,PPT敌手找到 $x$ 使得 $H^s(x)=y$ 是不可行的
- 抗碰撞 => 弱抗碰撞 => 单向
5.2 域扩张:Merkle-Damgard变换
用于将压缩函数扩展为完整的哈希函数,同时保持前者的抗碰撞性
-
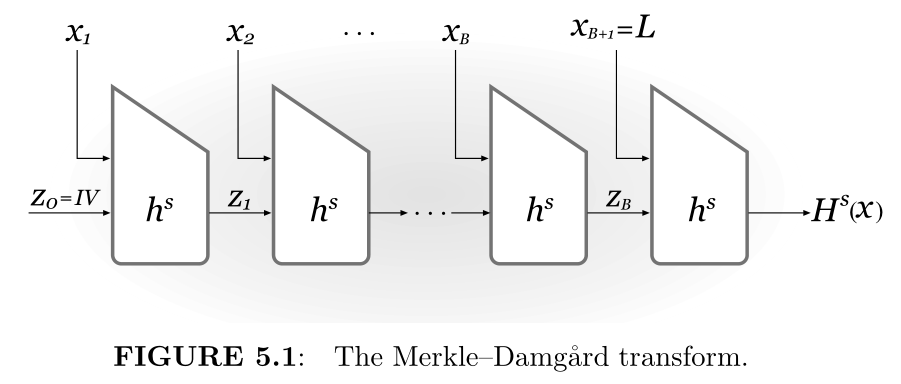
将定长输入的哈希函数通过Merkle-Damgard变换转换为任意长度输入的哈希函数,构造5.3:

-
定理5.4:如果 $(\mathsf{Gen},h)$ 是抗碰撞的,则 $(\mathsf{Gen},H)$ 也是抗碰撞的【证明on P157】【形式化证明on 练习5.4】
5.3 使用哈希函数实现消息认证
Hash-and-MAC
-
构造5.5:

-
定理5.6:若 $\Pi$ 是对长 $\ell$ 的消息安全的MAC,且 $\Pi_H$ 是抗碰撞的,则构造5.5是对任意长消息安全的MAC【证明on P160】
HMAC
-
构造5.7:

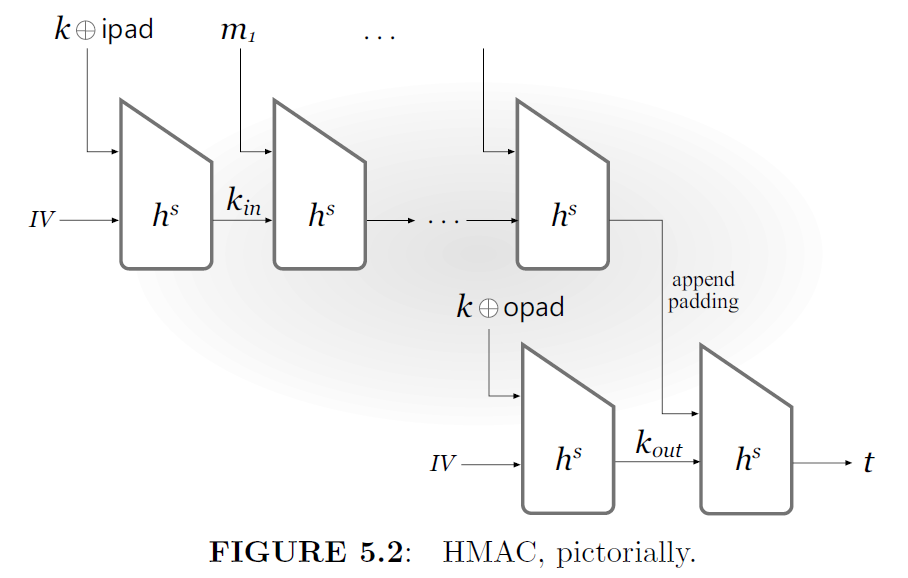
5.5 Random-Oracle模型
- 向oracle查询 $x$ 并得到输出 $y$ ,$x$ 是保密的,甚至查询oracle这个事件本身也是保密的
- 一致性:若对特定的输入 $x$ ,oracle输出 $y$ ,则之后再输入相同的 $x$ ,oracle仍然输出 $y$
- 一些性质:
- 若 $x$ 没有发送到 $H$ 进行查询,则 $H(x)$ 的值是均匀随机的
- 即使 $x$ 不是随机的,甚至 $x$ 是已知的, $H(x)$ 的值也是均匀随机的
- 若 $\mathcal{A}$ 向 $H$ 请求 $x$ ,则规约过程可以看到这个请求,也能知道 $x$
- 规约过程可以设置 $H(x)$ 的值,只要这个值是均匀随机分布的
- 若 $x$ 没有发送到 $H$ 进行查询,则 $H(x)$ 的值是均匀随机的
Random-Oracle实例
假设Random-Oracle将 $\ell_{in}$ 比特输入映射为 $\ell_{out}$ 比特输出,且 $\ell_{in},\ell_{out}>n$
- Random-Oracle作伪随机生成器($\ell_{in}<\ell_{out}$)
- $|Pr[\mathcal{A}{H(\cdot)}(y)=1]-Pr[\mathcal{A}{H(\cdot)}(H(x))=1]|\leq \mathsf{negl}(n)$ ,其中 $x\in{0,1}{\ell_{in}(n)},,y\in{0,1}{\ell{out}(n)}$
- Random-Oracle作抗碰撞哈希函数($\ell_{in}>\ell_{out}$)
- 任何PPT敌手 $\mathcal{A}$ 成功进行如下实验的概率可忽略:
- 选择随机函数 $F$
- $\mathcal{A}$ 获胜,当他输出不同的 $x,x’$ 使得 $H(x)=H(x’)$
- 任何PPT敌手 $\mathcal{A}$ 成功进行如下实验的概率可忽略:
Chapter 7: Theoretical Constructions of Symmetric-Key Primitives
7.1 单向函数
定义
- 逆转实验 $\mathsf{Invert}_{\mathcal{A},f}(n)$ :
- 随机均匀选择 $x\in{0,1}^n$ ,计算 $y:=f(x)$
- $\mathcal{A}$ 根据输入 $1^n$ 和 $y$ ,得到输出 $x’$
- 当 $f(x’)=y$ 时,实验的输出为1,否则输出0
- 定义7.1:函数 $f:{0,1}*\rightarrow{0,1}*$ 是单向函数,若满足:
- (计算简单)存在一个多项式时间算法 $M_f$ 来计算 $f$ ,即对所有 $x$ 有 $M_f(x)=f(x)$
- (求逆困难)对所有PPT算法 $\mathcal{A}$ 存在一个可忽略函数使得:
$$
Pr[\mathsf{Invert}_{\mathcal{A},f}(n)=1]\leq\mathsf{negl}(n)
$$
- 对于2,可以将其简记为:
$$
\underset{x\leftarrow{0,1}n}{Pr}[\mathcal{A}(1n,f(x))\in f^{-1}(f(x))]\leq\mathsf{negl}(n)
$$
- 定义7.2:PPT算法组成的元组 $\Pi=(\mathsf{Gen},\mathsf{Samp},f)$ 是一个函数族,若满足:
- 参数生成算法 $\mathsf{Gen}$ 根据输入 $1^n$ ,输出参数 $I,,|I|\geq n$ 。$I$ 中的每一个值定义了函数 $f_I$ 的定义域 $\mathcal{D}_I$ 和值域 $\mathcal{R}_I$
- 采样算法 $\mathsf{Samp}$ 根据输入 $1^n$ ,输出 $\mathcal{D}_I$ 的一个均匀分布的元素
- 评估算法(确定性)$f$ 根据输入 $I$ 和 $x\in\mathcal{D}_I$ ,输出 $y\in\mathcal{R}_I$ ,记作 $y:=f_I(x)$
- $\Pi$ 是一个排列族,若对所有 $\mathsf{Gen}(1^n)$ 输出的 $I$ 的值,满足 $\mathcal{D}_I=\mathcal{R}_I$ 且函数 $f_I:\mathcal{D}_I\rightarrow\mathcal{D}_I$ 是双射(单射且满射)
- 对函数族定义逆转实验 $\mathsf{Invert}_{\mathcal{A},\Pi}(n)$ :
- 运行 $\mathsf{Gen}(1^n)$ 来获取 $I$ ,运行 $\mathsf{Samp}(I)$ 来获取随机均匀 $x\in\mathcal{D}_I$ ,最后计算 $y:=f_I(x)$
- $\mathcal{A}$ 根据输入 $I,,y$,输出 $x’$
- 当 $f(x’)=y$ 时,实验的输出为1,否则输出0
- 定义7.3:函数族/排列族 $\Pi=(\mathsf{Gen},\mathsf{Samp},f)$ 是单向的,若对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{Invert}_{\mathcal{A},\Pi}(n)=1]\leq\mathsf{negl}(n)
$$
硬核谓词
- 定义7.4:函数 $\mathsf{hc}:{0,1}^*\rightarrow{0,1}$ 是函数 $f$ 的硬核谓词,若 $\mathsf{hc}$ 可以在多项式时间内计算,并且对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
\underset{x\leftarrow{0,1}n}{Pr}[\mathcal{A}(1n,f(x))=\mathsf{hc}(x)]\leq\frac{1}{2}+\mathsf{negl}(n)
$$- $\mathsf{hc}(x)$ 可以根据 $x$ 很容易算出,但很难根据 $f(x)$ 算出
7.2 单向函数构造伪随机
Step1:说明任何单向函数都存在硬核谓词
- 定理7.5(Goldreich–Levin定理):假设单向函数存在,则存在一个单向函数 $g$ 和一个 $g$ 硬核谓词 $\mathsf{hc}$
- 具体来说,令 $f$ 是一个单向函数,可以构造 $g(x,r)\overset{def}{=}(f(x),r),,|x|=|r|$ ,并定义:
$$
\mathsf{hc}(x,r)\overset{def}{=}\oplus^n_{i=1}x_i\cdot r_i
$$
Step2:说明单向排列的硬核谓词可以构造伪随机生成器
- 具体来说,令 $f$ 是一个单向函数,可以构造 $g(x,r)\overset{def}{=}(f(x),r),,|x|=|r|$ ,并定义:
- 定理7.6:令 $f$ 是一个单向排列,$\mathcal{hc}$ 是 $f$ 的硬核谓词,则 $G(s)\overset{def}{=}f(s)||\mathsf{hc}(s)$ 是扩张因子 $\ell(n)=n+1$ 的伪随机生成器
- 定理7.7:如果存在一个扩张因子 $\ell(n)=n+1$ 的伪随机生成器,则对任何多项式 $\mathsf{poly}$ 存在一个扩张因子为 $\mathsf{poly}(n)$ 伪随机生成器
Step3:根据伪随机生成器构造伪随机函数 - 定理7.8:如果存在一个扩张因子 $\ell(n)=2n$ 的伪随机生成器,则存在一个伪随机函数
- 定理7.9:如果存在一个伪随机函数,则存在一个强伪随机排列
- 推论7.10:假设存在单向函数,则存在任何扩张因子的伪随机生成器,伪随机函数,强伪随机排列
- 推论7.11:如果存在单向函数,则存在CCA-安全的对称加密方案以及安全的MAC
7.8 计算不可区分性
- 定义7.30:两个概率集合 $\mathcal{X}={X_n}{n\in\mathbb{N}}$ 和 $\mathcal{Y}={Y_n}{n\in\mathbb{N}}$ 是计算不可区分的,记作 $\mathcal{X}\overset{c}{\equiv}\mathcal{Y}$ ,若对所有PPT判别器 $D$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
|\underset{x\leftarrow X_n}{Pr}[D(1^n,x)=1]-\underset{y\leftarrow Y_n}{Pr}[D(1^n,y)=1]|\leq\mathsf{negl}(n)
$$- 概率集合是无穷多概率分布的序列
- 通常也会把 $\underset{x\leftarrow X_n}{Pr}[D(1^n,x)=1]$ 记作 $Pr[D(1^n,X_n)=1]$
- 计算不可区分具有传递性,即:若 $\mathcal{X}\overset{c}{\equiv}\mathcal{Y},,\mathcal{Y}\overset{c}{\equiv}\mathcal{Z}$ ,则 $\mathcal{X}\overset{c}{\equiv}\mathcal{Z}$
- 使用计算不可区分定义伪随机生成器——定义7.31:令 $\ell(\cdot)$ 是一个多项式,令 $G$ 是一个确定性多项式时间算法,且对所有 $s$ 满足 $|G(s)|=\ell(|s|)$ 。$G$ 是伪随机生成器若满足:
- (扩张)对所有 $n$ 满足 $\ell(n)>n$
- (伪随机)集合 ${G(U_n)}{n\in\mathbb{N}}$ 与 ${U{\ell(n)}}_{n\in\mathbb{N}}$ 在计算上不可区分
- 其中 $U_n$ 代表在 ${0,1}^n$ 上的均匀分布
- 令 $\mathcal{X}$ 和 $\mathcal{Y}$ 是计算不可区分的可采样概率集合,则对所有多项式 $p$ ,集合 $\overline{\mathcal{X}}={(X_n{(1)},…,X_n{p(n)})}{n\in\mathbb{N}}$ 和 $\overline{\mathcal{Y}}={(Y_n{(1)},…,Y_n{p(n)})}{n\in\mathbb{N}}$ 计算不可区分
Chapter 10: Key Management and the Public-Key Revolution
10.3 密钥交换和Diffie-Hellman协议
-
密钥交换实验 $\mathsf{KE}_{\mathcal{A},\Pi}^{\mathsf{eav}}(n)$ :
- 两个参与方使用 $1^n$ 来执行协议 $\Pi$ 。协议执行完会产生一个记录 $\mathsf{trans}$ ,包含双方交流的所有信息以及双方最终输出的密钥 $k$
- 随机均匀选择 $b\in{0,1}$ 。若 $b=0$ 则令 $\hat{k}:=k$ ,否则随机均匀选择 $\hat{k}\in{0,1}^n$
- $\mathcal{A}$ 根据收到的 $\mathsf{trans}$ 和 $\hat{k}$ ,输出一比特 $b’$
- 若 $b=b’$ 则实验输出1,否则输出0
-
定义10.1:密钥交换协议 $\Pi$ 对窃听者安全,若对所有PPT敌手存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{KE}_{\mathcal{A},\Pi}^{\mathsf{eav}}(n)=1]\leq\frac{1}{2}+\mathsf{negl}(n)
$$ -
构造10.2:(Diffie-Hellman协议)

- 其中 $\mathbb{G}$ 是一个循环群,$q$ 是 $\mathbb{G}$ 的阶,$g$ 是 $\mathbb{G}$ 的生成元
-
定理10.3:若 $\mathcal{G}$ 的决策Diffie-Hellman问题是困难的,则Diffie-Hellman协议对于窃听者是安全的【证明on P368】
- 其中决策Diffie-Hellman问题指:任何敌手给定 $g,gx,gy$ 都不能将共享密钥 $g^{xy}$ 与随机均匀的值区分
Chapter 11: Public-Key Encryption
11.2 定义
- 定义11.1:公钥加密方案是一个PPT算法的三元组 $(\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})$ :
- $\mathsf{Gen}$ 根据输入的安全参数 $1^n$ ,输出一对密钥 $(pk,sk)$
- $\mathsf{Enc}$ 根据输入的公钥 $pk$ 和消息 $m$ ,输出密文 $c$ ,记作 $c\leftarrow\mathsf{Enc}_{pk}(m)$
- $\mathsf{Dec}$ 根据输入的私钥 $sk$ 和密文 $c$ ,输出消息 $m$ 或者失败 $\bot$ ,记作 $m:=\mathsf{Dec}_{sk}©$
抵抗选择明文攻击
- 窃听不可区分实验 $\mathsf{PubK}^{\mathsf{eav}}_{\mathcal{A},\Pi}(n)$ :
- $(pk,sk)\leftarrow\mathsf{Gen}(1^n)$
- 敌手 $\mathcal{A}$ 获得公钥 $pk$ ,并输出一对等长的消息 $m_0,,m_1$
- 随机均匀选择 $b\in{0,1}$ ,计算 $c\leftarrow\mathsf{Enc}_{pk}(m_b)$ ,然后将挑战密文 $c$ 发送给 $\mathcal{A}$
- $\mathcal{A}$ 输出 $b’$ ,若 $b=b’$ 则实验输出1(敌手成功),否则输出0
- 定义11.2:一个公钥加密方案 $\Pi=(\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})$ 对窃听攻击者不可区分,若对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{PubK}_{\mathcal{A},\Pi}^{\mathsf{eav}}(n)=1]\leq\frac{1}{2}+\mathsf{negl}(n)
$$ - 命题11.3:若一个公钥加密方案对窃听攻击者不可区分,则它也是CPA-安全的
- 对于公钥加密而言,任何窃听敌手都可以获得公钥来加密明文
- 定理11.4:确定性公钥加密方案都不是CPA安全的
多消息加密
- LR-oracle实验 $\mathsf{PubK}^{\mathsf{LR-cpa}}_{\mathcal{A},\Pi}(n)$ :
- $(pk,sk)\leftarrow\mathsf{Gen}(1^n)$
- 随机均匀选择 $b\in{0,1}$
- 敌手 $\mathcal{A}$ 获得输入 $pk$ ,并且可以访问oracle $\mathsf{LR}_{pk,b}(\cdot,\cdot)$
- 敌手 $\mathcal{A}$ 输出一比特 $b’$
- 若 $b=b’$ 则实验输出1(敌手成功),否则输出0
- 其中oracle $\mathsf{LR}{pk,b}(\cdot,\cdot)$ :输入两个等长的消息 $m_0$ ,$m_1$ ,若 $b=0$ 输出 $c\leftarrow \mathsf{Enc}{pk}(m_0)$ ;若 $b=1$ 输出 $c\leftarrow \mathsf{Enc}_{pk}(m_1)$
- 定义11.5:一个公钥加密方案 $\Pi=(\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})$ 对窃听攻击者是多消息不可区分的,若对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{PubK}_{\mathcal{A},\Pi}^{\mathsf{LR-cpa}}(n)=1]\leq\frac{1}{2}+\mathsf{negl}(n)
$$ - 定理11.6:若一个公钥加密方案是CPA-安全的,则它也是多消息不可区分的【*证明on P383】
- 断言11.7:$\Pi=(\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})$ 是对一比特消息进行加密的公钥加密方案,$\Pi’=(\mathsf{Gen’},\mathsf{Enc’},\mathsf{Dec’})$ 是对任意长消息进行加密的公钥加密方案,构造如下:$\mathsf{Enc’}{pk}(m)=\mathsf{Enc}{pk}(m_1),…,\mathsf{Enc}{pk}(m{\ell})$ ,其中 $m=m_1\cdot\cdot\cdot m_{\ell}$ 。则如果 $\Pi$ 是CPA-安全的,$\Pi’$ 也是
抵抗选择密文攻击
- CCA不可区分实验 $\mathsf{PubK}^{\mathsf{cca}}_{\mathcal{A},\Pi}(n)$ :
- $(pk,sk)\leftarrow\mathsf{Gen}(1^n)$
- 敌手 $\mathcal{A}$ 获得 $pk$ ,并且可以访问解密oracle $\mathsf{Dec}_{sk}(\cdot)$ 。$\mathcal{A}$ 输出一对等长消息 $m_0,m_1$
- 随机均匀选择 $b\in{0,1}$ ,计算 $c\leftarrow\mathsf{Enc}_{pk}(m_b)$ 并发送给 $\mathcal{A}$
- $\mathcal{A}$ 可以继续与解密oracle交互,但不能解密 $c$ 。最终 $\mathcal{A}$ 输出一比特 $b’$
- 若 $b=b’$ 则实验输出1(敌手成功),否则输出0
- 定义11.8:一个公钥加密方案 $\Pi=(\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})$ 是CCA-安全的,若对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{PubK}_{\mathcal{A},\Pi}^{\mathsf{cca}}(n)=1]\leq\frac{1}{2}+\mathsf{negl}(n)
$$- 若一个公钥加密方案是CCA-安全的,则它也是多消息CCA-安全的
11.3 混合加密和KEM/DEM范式
-
定义11.9:一个密钥封装机制(KEM)是PPT算法的三元组 $(\mathsf{Gen},\mathsf{Encaps},\mathsf{Decaps})$ 使得:
- 密钥生成算法 $\mathsf{Gen}$ 根据输入的安全参数 $1^n$ ,输出公私钥对 $(pk,sk)$
- 密封算法 $\mathsf{Encaps}$ 根据输入的安全参数 $1^n$ 和公钥 $pk$ ,输出密文 $c$ 和密钥 $k\in{0,1}^{\ell(n)}$ ,其中 $\ell$ 是密钥长度。记作 $(c,k)\leftarrow\mathsf{Encaps}_{pk}(1^n)$
- 确定性的解封算法 $\mathsf{Decaps}$ 根据输入的私钥 $sk$ 和密文 $c$ ,输出密钥 $k$ 或者一个特殊符号 $\bot$ 来表示解封失败。记作 $k:=\mathsf{Decaps}_{sk}©$
-
构造11.10:

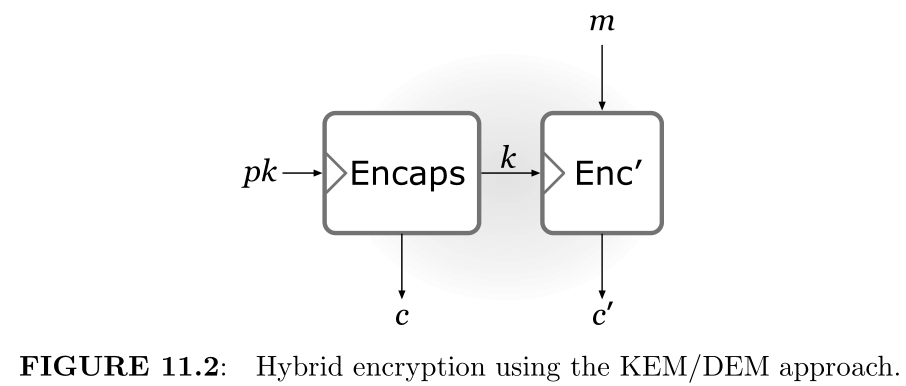
CPA-安全
- 令 $\Pi=(\mathsf{Gen},\mathsf{Encaps},\mathsf{Decaps})$ 是KEM,定义CPA不可区分实验 $\mathsf{KEM}^{\mathsf{cpa}}_{\mathcal{A},\Pi}(n)$ :
- $(pk,sk)\leftarrow\mathsf{Gen}(1^n)$ ,然后 $(c,k)\leftarrow\mathsf{Encaps}_{pk}(1^n)$ ,其中 $k\in{0,1}^n$
- 随机均匀选择 $b\in{0,1}$ 。若 $b=0$ 则令 $\hat{k}:=k$ ,若 $b=1$ ,则随机均匀选择 $\hat{k}\in{0,1}^n$
- $\mathcal{A}$ 获得 $(pk,c,\hat{k})$ ,并输出 $b’$ 。若 $b=b’$ 则实验输出1(敌手成功),否则输出0
- 定义11.11:一个KEM $\Pi$ 是CPA-安全的,若对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{KEM}_{\mathcal{A},\Pi}^{\mathsf{cpa}}(n)=1]\leq\frac{1}{2}+\mathsf{negl}(n)
$$ - 定理11.12:若 $\Pi$ 是一个CPA-安全的KEM,$\Pi’$ 是一个对窃听攻击不可区分的对称加密方案,则构造11.10中的 $\Pi^{\mathsf{hy}}$ 是CPA-安全的公钥加密方案【证明on P394】
CCA-安全
- 令 $\Pi=(\mathsf{Gen},\mathsf{Encaps},\mathsf{Decaps})$ 是KEM,定义CCA不可区分实验 $\mathsf{KEM}^{\mathsf{cca}}_{\mathcal{A},\Pi}(n)$ :
- $(pk,sk)\leftarrow\mathsf{Gen}(1^n)$ ,然后 $(c,k)\leftarrow\mathsf{Encaps}_{pk}(1^n)$ ,其中 $k\in{0,1}^n$
- 随机均匀选择 $b\in{0,1}$ 。若 $b=0$ 则令 $\hat{k}:=k$ ,若 $b=1$ ,则随机均匀选择 $\hat{k}\in{0,1}^n$
- $\mathcal{A}$ 获得 $(pk,c,\hat{k})$ 以及可以访问oracle $\mathsf{Decaps}_{sk}(\cdot)$ ,但不能请求解封挑战密文 $c$
- $\mathcal{A}$ 输出 $b’$ 。若 $b=b’$ 则实验输出1(敌手成功),否则输出0
- 定义11.13:一个KEM $\Pi$ 是CCA-安全的,若对所有PPT敌手 $\mathcal{A}$ 存在一个可忽略函数 $\mathsf{negl}$ 使得:
$$
Pr[\mathsf{KEM}_{\mathcal{A},\Pi}^{\mathsf{cca}}(n)=1]\leq\frac{1}{2}+\mathsf{negl}(n)
$$ - 定理11.14:若 $\Pi$ 是一个CCA-安全的KEM,$\Pi’$ 是一个CCA-安全的对称加密方案,则构造11.10中的 $\Pi^{\mathsf{hy}}$ 是CCA-安全的公钥加密方案
