论文阅读-Ekiden. A Platform for Confidentiality-Preserving, Trustworthy, and Performant Smart Contracts

Schenk

Paper ReadingSGX

更新于：2022年7月20日

字数：7.3k字

时长：27分钟

次浏览

1.引入

现有的智能合约系统因此缺乏保密性和隐私性，它们不能安全地存储或计算敏感数据；区块链共识需求也使得智能合约在计算能力、存储容量和事务吞吐量方面的性能低下。

区块链和TEE有互补特性：

• 区块链可以保证强可用性和持久性，而TEE不能保证可用性（因为宿主可以自行决定终止TEE），也不能可靠地访问网络或持久性存储
• 区块链的计算能力非常有限，必须公开其整个状态以供公共验证，而TEE与本地计算相比产生的开销很小，并通过远程认证提供具有机密性的可验证计算

区块链和TEE结合会产生新的安全问题：由于TEE的基本限制是恶意主机可以任意操纵它的调度和I/O，TEE可能在任意时间中止，导致区块链上丢失和冲突的状态。TEE缺少可信时钟，因此很难更新到区块链的最新状态。可能存在的攻击例如针对区块链的完整性攻击危及TEE保护内容的机密性（如，攻击者可以通过提供一个伪造的区块链来绕过TEE强制执行的隐私计算，以退回到执行前并向其请求任意多个查询）

Ekiden采用计算与共识分离的架构。Ekiden在链下的TEE中使用计算节点执行私有数据的智能合约计算（避免了链上计算负担），然后验证它们在链上的正确执行，而区块链上的共识节点不需要使用TEE。Ekiden与共识机制无关，只需要一个能够验证来自计算节点的远程认证的区块链。

为了解决TEE的可用性和网络安全限制，Ekiden支持链上检查和合约状态存储。

主要贡献

• 正式安全建模：使用一个理想的功能$F_{Ekiden}$来表达Ekiden的全部安全需求，在通用可组合性(UC)框架中概述安全性证明，表明Ekiden协议在并发组合下与$F_{Ekiden}$匹配；
• TEE-区块链结合方案：系统地列举了区块链和TEE融合产生的基本缺陷，并提供了克服这些缺陷的通用技术；
• 性能：区块链可能是TEE-区块链混合系统的性能瓶颈。论文提供了优化，在不降低安全性的情况下最小化区块链的使用。

2.背景

智能合约

智能合约系统的限制：

• 对每个节点都完全复制的智能合约进行链上计算很昂贵
• 传统的智能合约系统不提供隐私保护，用户由假名区别，但是假名只提供很弱的隐私保护
• 合约状态和用户输入必须是公开的，以便矿工验证正确的计算，缺乏隐私

可信硬件

• SGX生成的认证是不可伪造的
• 单单SGX不能保证可用性（恶意主机可以任意终止Enclave或丢弃消息）
• SGX容易遭受侧信道攻击

3.TEE-区块链系统的技术挑战

容忍TEE故障

可用性故障

在SGX中，恶意主机可以终止Enclave，即使是诚实主机也可能在电源循环中丢失Enclave。TEE-区块链系统必须能够容忍这样的主机故障，确保崩溃的TEE可以延迟执行。

论文将TEE视为可消耗和可互换的，依赖区块链来解决并发性导致的任何冲突。为了确保任何特定的TEE很容易被替换，TEE是无状态的，并且任何持久状态都由区块链存储。

侧信道

为了对付SGX的侧信道攻击，论文采用的方法是在空间和时间上进行划分，针对强敌手模型设计Ekiden中的关键组件，如密钥管理器，允许攻击者打破一小部分TEE的机密性，并限制其他组件对密钥管理器的访问。另外还采用了主动密钥旋转来限制泄漏密钥的权限。

时钟故障

SGX的时钟不可信，一个TEE-区块链混合协议必须尽量减少对TEE时钟的依赖。

在论文的设计中，不需要TEE拥有当前区块链的状态。具体来说，不需要TEE来区分陈旧状态和当前状态，而依赖于区块链主动拒绝任何陈旧输入状态的更新。

PoW区块链的发布证明

为了利用区块链作为持久存储，TEE必须能够有效地验证一个项目已经存储在区块链中，同时TEE也需要能够验证新块。这就需要一个可信时钟来防止敌手隔离Enclave而提供一个无效的子链。

论文利用了TEE的保密性，这样延迟时钟响应的攻击者就不能阻止Enclave成功验证区块链内容。

TEE中的密钥管理

使用区块链持久化TEE状态的一个基本限制是缺乏保密性。通常可以通过在多个TEE中保存相同的密钥副本来实现密钥存储，虽然这种方法能很好地抵抗状态丢失，但是会造成更大的攻击面，在可用性和暴露风险之间需要权衡。

论文针对强敌手模型设计密钥管理器，允许攻击者打破一小部分TEE的机密性，并限制其他组件对密钥管理器的访问。

执行结果的原子性交付

通常，对于有状态的TEE-区块链协议，TEE的执行产生两个消息：

• $m_1$：向调用者发送输出结果
• $m_2$：向区块链发送状态更新

这两个消息必须原子性交付，要么都交付成功，有一个交付失败则系统不可用：$m_1$ 在调用者收到时交付成功，$m_2$ 在区块链接受时交付成功，被拒绝的状态更新不是交付成功。

若不要求两个消息的原子性交付，可能产生的攻击有：

• 如果只有 $m_1$ 被交付，可能会产生倒回攻击，由于TEE不能判断输入状态是否为新状态，因此攻击者可以提供旧状态以从旧状态恢复TEE的执行，直到获得想要的结果（公平性）；
• 如果只有 $m_2$ 被交付，用户可能永久丢失输出，因为一般不可能根据更新后的状态来重新产生相同的输出

4.Ekiden概述

为了支持像信用评分这样的大规模隐私敏感应用程序，智能合约系统满足数据机密性保护以及高性能的同时要保持区块链提供的完整性和可用性。

Ekiden概述

Ekiden实现了用户自定义智能合约的安全执行环境，Ekiden合约是一个确定性的有状态程序。将合约程序的形式定义为 $(outp,st_{new}):=Contract(st_{old},inp)$ ，其中合约的输入是 $st_{old}$（前一个状态）和 $inp$（用户输入），生成输出 $outp$ 和新状态 $st_{new}$。

一旦部署在Ekiden上，智能合约就有了强大的保密性、完整性和可用性保证。在Ekiden中，有三种实体：

• 客户是智能合约的用户，在Ekiden中，客户可以通过秘密输入创建合同或执行现有的合同。无论哪种情况，客户机都将计算委托给计算节点；
• 计算节点在合约TEE中执行合约并且生成用于证明状态更新正确性的证明，从而处理客户的请求。一组计算节点组成一个密钥管理委员会，并运行一个分布式协议来管理合约TEE使用的密钥，合约TEE通过密钥管理委员会来创建或恢复密钥；
• 共识节点构成区块链，合约状态和认证都保存在这个区块链上。共识节点负责使用TEE检查状态更新的有效性。

工作流程

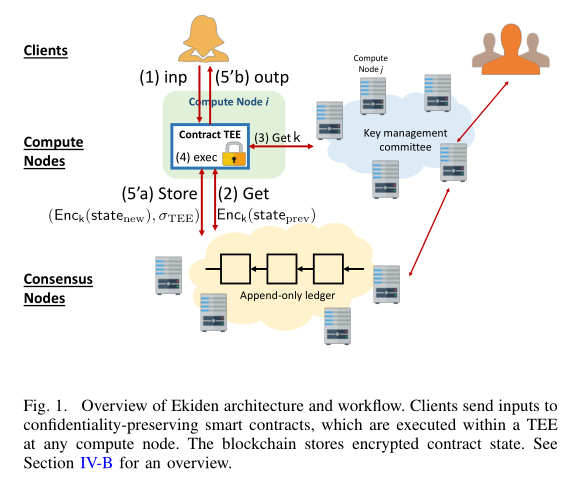
简单起见，假设客户拥有使用的计算节点的优先级列表，客户记为 $P$ ，计算节点记为 $Comp$。

合约创建

创建合约时，$P$ 将合约代码 $contract$ 发送给 $Comp$，$Comp$ 将 $Contract$ 加载到合约TEE中，合约TEE创建一个新鲜的合约id $cid$，从密钥管理委员会获取新鲜的 $(pk^{{in}_{cid},sk}{in}{cid})$ 对和 $k{cid}^{state}$ 并生成加密的初始状态 $Enc(k^{state}{cid},\vec{0})$ 和一个证明 $\sigma{TEE}$（用于证明TEE初始化的正确性以及 $pk_{cid}^{in}$ 是对应于合约 $cid$ 的公钥）。

最后，$Comp$ 从认证服务获取 $\sigma_{TEE}$ 的正确性证明，该证明和 $\sigma_{TEE}$ 绑定到一个“certified”证明 $\pi$ 中。$Comp$ 接着发送 $(Contract,pk^{{in}_{cid},Enc(k}{state}_{cid},\vec{0}),\pi)$ 到共识节点。

合约创建的完整协议由Fig2的 $Prot_{Ekiden}$ 中的 create 表示。

请求执行

描述Fig1的过程：

(1) 为了使用输入 $inp$ 来执行合约 $cid$ ，$P$ 首先从区块链获取与合约 $cid$ 相关联的 $pk_{cid}^{in}$ ，计算 $inp_{ct}=Enc(pk^{in}{cid},inp)$ ，并将消息 $(cid,inp{ct})$ 发送给 $Comp$ 。如 $Prot_{Ekiden}$ 的Line8-11所示。

(2) $Comp$ 从区块链取出合约代码，以及合约 $cid$ 的加密过去状态 $st_{ct}=Enc(k^{state}{cid},st{old})$ ，并将 $st_{ct}$ 和 $inp_{ct}$ 加载到TEE中执行。 如 $Prot_{Ekiden}$ 的Line30-33所示。

(3-4) 合约TEE从密钥管理委员会获取 $k_{cid}^{state}$ 和 $sk^{in}{cid}$ ，并使用它们解密 $st{ct}$ 和 $inp_{ct}$ 。从而生成输出 $outp$ ，一个新的加密状态 $st^{{'}_{ct}=Enc(k_{cid}}{state},st_{new})$ 和一个用于证明计算正确的签名 $\pi$ 。如 $Prot_{Ekiden}$ 的Line7-13所示。

(5a, 5b) 最后，$Comp$ 和 $P$ 执行一个原子交付协议，将 $outp$ 交付给 $P$ ，并将 $(st^{'}{ct},\pi)$ 交付给共识节点。共识节点先验证 $\pi$ 再接受新状态 $st^{'}{ct}$ 并将其存放在区块链上，只有在这之后，$P$ 才能接收到 $outp$ 。

Ekiden将请求执行与共识解耦。在以太坊中，请求执行被网络中的所有节点复制以达成共识，使得整个网络的速度和单个节点一样慢。而在Ekiden中，请求只被K个计算节点执行，K通常比较小，共识节点只需要验证K个正确执行的证明。

论文的实现中，使用签名 $\pi$ 来作为TEE正确执行的证明。一个计算节点 $Comp$ 通过如下方式获得签名 $\pi$ 。假设 $Comp$ 执行结果为一个输出 $st^{‘}{ct}$ 和一个证明 $\sigma{TEE}$（对合约代码和 $st^{’}{ct}$ 的签名），$Comp$ 将 $\sigma{TEE}$ 发送到IAS，IAS验证 $\sigma_{TEE}$ 并回复 $\pi=(b,\sigma_{TEE},\sigma_{IAS})$ ，其中 $b\in{0,1}$ 表明 $\sigma_{TEE}$ 的有效性，$\sigma_{IAS}$ 是IAS对 $b$ 和 $\sigma_{TEE}$ 的签名。然后 $\pi$ 被提交到共识节点作为 $st^{'}_{ct}$ 正确性的证明。

Ekiden安全目标

• 正确执行：合约状态转换反映了合约代码在给定状态和输入上的正确执行；
• 一致性：在任何时候，区块链都存储与每个计算节点一致的单一状态转换序列；
• 保密：Ekiden保证合约状态和来自诚实客户的输入对所有其他各方保密，另外Ekiden也能抵御一些密钥管理TEE的背叛；
• 优雅的机密性降级：如果有计算节点违反机密性，Ekiden提供前向保密，并与受影响的TEE进行合理隔离。假设机密性违反发生在 $t$ ，攻击者最多能够获取 $t-\Delta$ 的历史。

Ekiden不对合约级别的隐私泄露进行防御，如合约中的隐蔽信道、bug或侧信道。

假设和威胁模型

TEE

假设SGX是正确实现和安全制造的，但由于SGX存在侧信道攻击，假设敌手可以危及一小部分TEE的机密性。

区块链

Ekiden对底层共识协议不可知。假设区块链正确执行规定的计算，并且总是可用的。Ekiden依赖共识节点来进行认证，进一步假设区块链提供发布证明，可以证明区块链上包含一些内容。

威胁模型

• 系统中的各方都必须信任Ekiden和TEE
• 假设敌手可以控制除了一个计算节点之外的所有操作系统和网络堆栈，在受控节点上，敌手可以任意排序消息和调度进程
• 敌手可以操控任意数量的客户
• 客户不需要自己执行合约，也不需要可信硬件
• 诚实用户信任自己的代码和平台，但不相信其他客户
• 每个合约都有一个明确的策略来规定如何处理数据和服务请求
• Ekiden不能防止合约有意或无意地通过软件漏洞泄露机密

5.Ekiden重要模块

发布证明

为permissionless的区块链提出发布证明协议：

发布证明是一种在验证者 $\varepsilon$ 、合约TEE和不可信证明提供者 $P$ 之间的交互式证明。总的来说，只给 $P$ 有限的时间在足够困难的子链的块上发布消息，从而敌手很难伪造。

$\varepsilon$ 存储最近的一个checkpoint块 $CB$，可以通过 $CB$ 计算难度系数 $\delta(CB)$ ， $\varepsilon$ 向任何请求客户发出 $CB$ 版本，使客户能够验证 $CB$ 的新鲜度。给定一个有效的最近的 $CB$ ， $\varepsilon$ 可以通过 $\delta(CB)$ 来验证新的块。为了方便分析，论文中的难度系数是恒定的。

为了初始化 $m$ 的发布，$\varepsilon$ 获取时间戳 $t_1$ ， $\varepsilon$ 可能需要经过一段延时才能收到 $t_1$ 。收到 $t_1$ 之后，$\varepsilon$ 生成一个随机数 $r$ 并要求 $P$ 发布 $(m,r)$ 。$\varepsilon$ 收到 $P$ 发送的证明 $\pi_{(m,r)}$ 之后，获取时间戳 $t_2$ 。令 $n_c$ 为发布 $(m,r)$ 所需要的确认次数，$\tau$ 为期望的块间隔时间（区块链中的定值），$\epsilon$ 为一个乘法松弛因子，代表块产生的时间变化。例如，$\epsilon=1.5$ 表示 $\pi_{(m,r)}$ 的产生可以比预期在主链上的速度慢1.5倍。$\varepsilon$ 只有当 $t_2-t_1<n_c\times\tau\times\epsilon$ 时才接受 $\pi_{(m,r)}$。

将 $\epsilon$ 设置为一个大的值可以降低错误拒绝的概率（拒绝诚实用户 $P$ 的证明会导致区块链增长速度减慢），然而大的 $\epsilon$ 值也会导致错误接受的概率增大。对于 $\epsilon>1$ ，需要一个足够大的 $n_c$ 来使成功攻击的概率可忽略，然而大的 $n_c$ 意味着诚实用户 $P$ 需要等待很长时间才能获得输出，影响用户体验。

例如，假设攻击者有25%的算力，设置 $n_c=80$ 以及 $\epsilon=1.6$ 意味着攻击者需要预期2¹¹²次哈希才能伪造一个发布证明，而诚实的证明只有2^-19的几率被拒绝。攻击者的伪造时间只有 $t_2-t_1$ ，而若 $\varepsilon$ 经过一段延时才收到 $t_1$ ，则 $t_2-t_1$ 就更短，对攻击者不利。

一旦一条消息在一个TEE中发布，其他TEE可以通过经认证的安全信道获取该消息及其证明，从而节省重复协议的成本。

密钥管理

每个Ekiden合约都和一系列密钥相关联，包括一个用于状态加密的对称密钥和用于加密客户输入的密钥对。

敌手模型

• 假设敌手可以打破一定比例（$f%$）的TEE的机密性
• 假设参与主体有抵御女巫攻击的身份（交押金才能参与协议）
• 假设随时有足够多（$2f%$）的用户在线，从而密钥的可用性得到保证（通过经济奖惩来激励参与）

所需属性

由于解密密钥最终会暴露给合约TEE，而合约TEE本身也可能受到威胁，因此采用的密钥必须是短期的，来自暴露机会更低的的长期主密钥。密钥管理协议应满足的属性：

• 机密性：敌手无法窃取长期主密钥
• 可用性：诚实的合约TEE能获取解密密钥
• 前向保密：如果一个短期密钥被窃取，它不能用于解密早于 $t-\Delta$ 时间的加密消息

初步准备

• 分布式密钥生成（DKG）：DKG协议允许N个团体生成随机密钥，DKG协议允许的结果是一个秘密，通过秘密共享方案在各方之间共享；

• 分布式伪随机函数（PRF）：PRF是函数 $F={f_s}{s\in{S}}$ 的集合，并且对于随机索引 $s\leftarrow$S$，$f_s(·)$ 于一个随机函数不能区分。

  令 $G$ 是一个Schnorr group，$g$ 是一个生成器，$H:{0,1}^*\rightarrow G$ 是一个哈希函数，则 $f_s(x)=H(x)^s$ 是PRF族。

  假设 $s$ 被多方采用 $(k,n)$-秘密分享方案分享，为了评估 $f_s(x)$ ，团体 $i$ 计算并输出 $y_i=H(x)^{s_i}$ ，在收集了至少 $k+1$ 的 ${y_i}$ 之后，可以通过多项式插值得到 $f_s(x)$：$f(x)=H(x)^S=H(x){\sum_{i\in A}{S_i\lambda_i}}=\prod_{i\in A}{y_i^{\lambda_i}}$ ，其中 $\lambda_i$ 是拉格朗日系数 $\lambda_i=\prod_{j\neq i}{\frac{-i}{i-j}}$ 。

协议

• 密钥管理委员会和长期密钥：对于抵抗女巫攻击的身份，可以抽取N 个节点来形成密钥管理委员会（KMC），其中N是系统参数。初始化一个合约 $c$ 时，KMC运行DKG协议来生成一个长期密钥 $k_c$ ，从而 $k_c$ 通过 $(\lceil fN\rceil,N)$-秘密分享方案在KMC成员之间秘密分享。
• 生成短期密钥：假设短期密钥在每一轮都过期，为了在第 $t$ 轮获得合约 $c$ 的短期密钥，一个计算节点 $Comp$ 首先建立安全信道并与KMC成员认证身份。一旦验证了 $Comp$ 确实在执行 $c$ ，每个KMC成员 $i$ 计算 $k_{c,t,i}=H(t)^{k_ci}$ ，并将 $k_{c,t,i}$ 发送给 $Comp$ 。在从 $A\subseteq$ KMC 收集了 $f+1$ 个结果之后，$Comp$ 可以生成第 $t$ 轮的短期密钥 $k_{c,t}=\prod_{i\in A}{k_{c,t,i}^{\lambda_i}}$ ，其中 $\lambda_i$ 是拉格朗日系数 。
• 违规隔离：通过为每个计算节点强制执行隐私预算，主动隔离违反机密性的行为。为此，假设每个合约TEE有不可伪造的身份，密钥管理节点为每个计算节点 $Comp$ 维护一个计数器 $K_{Comp}$ 来记录请求次数。计数器会随着轮次增加而清零。只有当 $K_{Comp}<K$ 时密钥管理节点才满足计算节点的请求，其中 $K$ 是一个系统参数。这样，无论一个被破坏的计算节点产生多少个TEE，它最多只能获得 $K$ 个密钥。

原子性交付

假设TEE和调用客户 $P$ 之间有一个安全信道，通过以下协议实现 $m_1$ 和 $m_2$ 的原子交付：

1. TEE从密钥管理器获取新鲜的密钥 $k$ ，并将加密的认证消息 $m_1^c=Enc(k,m_1)$ 发送给 $P$ ;
2. 一旦 $P$ 确认收到 $m_1^c$ ，TEE将 $m_2$ 发送给区块链；
3. TEE得到 $m_2$ 的发布证明 $\pi_{m_2}$ 之后，将 $k$ 发送给 $P$。

6.协议细节和安全证明

$Prot_{Ekiden}$ 的目的是实现一个通用可组合性(UC)理想功能 $F_{Ekiden}$ 。

初步准备和符号说明

认证执行

使用 $G_{att}$ 正式定义可信硬件上经过验证的执行。一个party首先将程序 $prog$ 通过 install 消息加载进TEE中，通过 resume 调用，程序根据给定输入运行，生成输出 $outp$ 以及一个硬件密钥 $sk_{TEE}$ 下的签名认证 $\sigma_{TEE}=\sum_{TEE}.Sig(sk_{TEE},(prog,outp))$ ，其中 $sk_{TEE}$ 可以通过 $G_{att}.getpk()$ 获取。

如果一个TEE程序产生一对输出 $(outp_1,outp_2)$ ，认证只对 $outp_1$ 签名，即 $\sigma_{TEE}=\sum_{TEE}.Sig(sk_{TEE},(prog,outp_1))$ ，在 $outp_1$ 中包含 $outp_2$ 的哈希。

使用合约包装器来抽象例行常用功能，如状态加密，密钥管理等。被包装器扩充的合约 $c$ 称为 $\widehat{c}$ 。

区块链

$F_{blockchain}[succ]$ 定义了区块链，参数 $succ$ 指定添加到存储中的新item的条件，对交易有效性的概念进行建模。

除了读写接口，$F_{blockchain}$ 提供了一个接口使得客户可以确定一个item是否包含在区块链内，这个接口避免了提前下载整个区块链。

参数化 $F_{blockchain}$

在Ekiden中，存储的内容被解析为状态转换的有序数组，定义为 $trans_i=(H(st_{i-1}),st_i,\sigma_i)$ ，包含之前状态的哈希，新状态和对状态转换的正确性的TEE证明。存储可以被解释为一种特殊的初始状态，随后是一系列状态转换：$Storage=((Contract,st_0,\sigma_0),{trans_i}_{i\geq1})$ 。

状态转换必须扩展最新的状态，并且认证经过验证，它才是有效的。有效性验证是通过使用函数 $succ(·,·)$ 参数化 $F_{blockchain}$ 来实现的：当且仅当 $h=H(st_{old})$ 其中 $st_{old}$ 是 $Storage$ 中的最新状态，同时满足 $\sum_{TEE}.Vf(pk_{TEE},\sigma_{TEE},(h,st_{new}))$ 时，$succ(Storage,(h,st_{new},\sigma_{TEE}))=true$ 。这保证了状态转换链不会分叉。

协议的正式规范

$Prot_{Ekiden}$ 是Ekiden协议的正式规范，依赖 $G_{att}$ 和 $F_{blockchain}$ 作为认证执行和区块链的理想功能。$Prot_{Ekiden}$ 使用电子签名方案 $\sum(KGen,Sig,Vf)$ ，对称加密方案 $S\varepsilon(KGen,Enc,Dec)$ 以及非对称加密方案 $A\varepsilon(KGen,Enc,Dec)$。

状态密钥分享

每个合约都和一系列密钥绑定，合约TEE将管理密钥的工作委托给密钥管理TEE。在 $Prot_{Ekiden}$ 中，密钥管理的通信由 $keyManager$ 函数进行抽象。

合约创建

创建Ekiden中的合约时，客户 $P_i$ 输入合约代码 $Contract$ ，并调用计算节点 $Comp$ 的 create 子程序。$Comp$ 将 $\widehat{Contract}$ 加载进TEE中，并调用 create 进行初始化。如Fig9所示，合约TEE创建一个新鲜的合约 $cid$ ，从密钥管理器获得新鲜的 $(pk_{cid}^{in},sk{in}{cid})$ 和 $k{cid}^{state}$ ，并生成加密初始状态 $st_0$ 和一个证明 $\sigma_{TEE}$ ，$\sigma_{TEE}$ 证明了 $st_0$ 被正确初始化以及 $pk_{cid}^{in}$ 是合约 $cid$ 的对应公钥。计算节点 $Comp$ 将 $(Contract,cid,st_0,pk_{cid}^{in},\sigma_{TEE})$ 发送到 $F_{blockchain}$ 并等待回复。$Comp$ 将合约 $cid$ 返回给 $P_i$ ，然后 $P_i$ 验证合约 $cid$ 确实存储在 $F_{blockchain}$ 上。

请求执行

为了执行合约 $cid$ ，客户 $P_i$ 首先从 $F_{blockchain}$ 获得输入加密密钥 $pk_{cid}^{in}$ 。然后 $P_i$ 输入 $(cid,inp_{ct})$ 其中 $inp_{ct}$ 是经过 $pk^{in}{cid}$ 加密和经过 $spk_i$ 认证的 $P_i$ 的输入，并调用 $Comp$ 的 request 子程序。$Comp$ 从 $F{blockchain}$ 获取加密的之前状态 $st_{ct}$ ，并使用 $\widehat{Contract}$ 代码和输入 $(cid,inp_{ct},st_{ct})$ 启动一个合约TEE。

如Fig9所示，如果 $\sigma_{P_i}$ 验证通过，合约TEE使用从密钥管理器获得的密钥解密 $st_{ct}$ 和 $inp_{ct}$ ，并且执行合约 $Contract$ 得到结果 $(st_{new},outp)$ 。为了确保新状态和输出的原子性交付，$Comp$ 和 $P_i$ 执行第5章中描述的原子交付协议：

• 首先合约TEE计算 $outp_{ct}=Enc(k^{out}{cid},outp)$ 以及 $st{ct}^{'}=Enc(k{state}{cid},st{new})$ ，并且通过 $epk_i$ 建立的安全信道发送两个结果的认证给 $P_i$ ；
• $P_i$ 通过调用 $Comp$ 的 claim-output 子程序来确认接收，该子程序使得合约TEE发送 $m_1=(st_{ct}^{'},outp_{ct},\sigma)$ 到 $F_{blockchain}$ 。$\sigma$ 保护 $m_1$ 的完整性，并以加密方式将新状态和输出绑定到以前的状态和输入，从而恶意的 $Comp$ 无法篡改它；
• 一旦 $m_1$ 被 $F_{blockchain}$ 接受，合约TEE通过安全信道将解密后的 $outp_{ct}$ 发送给 $P_i$ 。

$Prot_{Ekiden}$ 的安全

定理1的证明在附录B

定理1（$Prot_{Ekiden}$ 的安全性）：

假设 $G_{att}$ 的认证方案 $\sum_{TEE}$ 和数字签名 $\sum$ 在选择消息攻击（EU-CMA）下不可伪造，$H$ 是弱抗碰撞性的，$A\varepsilon$ 和 $S\varepsilon$ 是IND-CPA安全的。则 $Prot_{Ekiden}$ 在 $(G_{att}, F_{blockchain})$-结合模型中安全地实现了对静态敌手的 $F_{Ediden}$ 。

减轻应用程序级别泄露

Ekiden通过启用持久化的应用程序状态来减少应用程序级的隐私泄露（由于智能合约编写的问题导致的隐私泄露等）。

7.实现

使用Rust SGX SDK实现了一个编译器，它可以自动将合约构建为可执行文件，并加载到计算节点中。

Ekiden与许多现有的区块链兼容。

应用

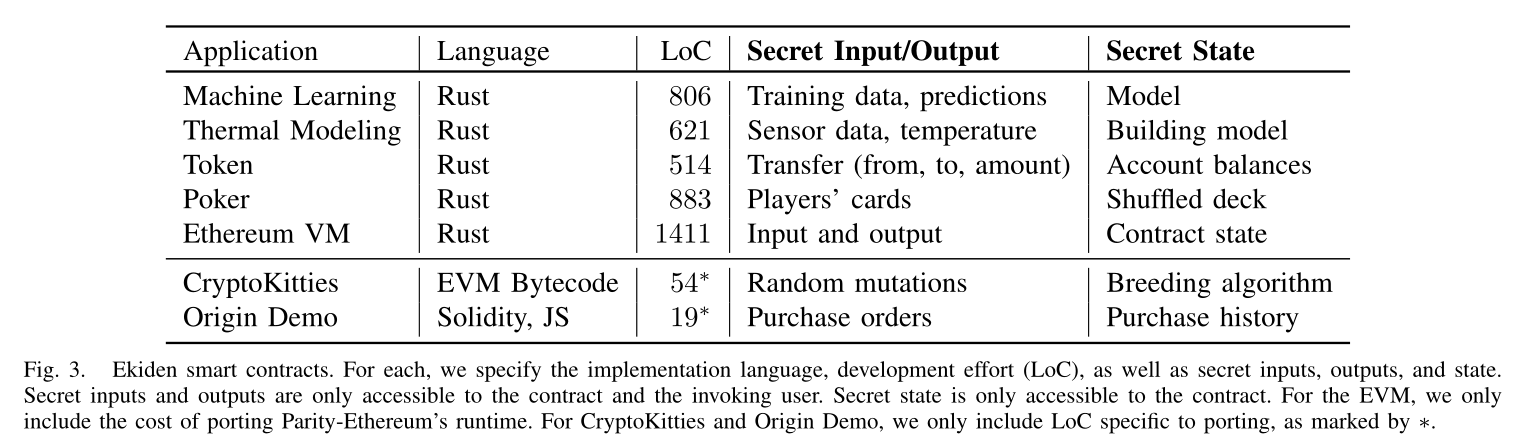
机器学习合约

为了演示对秘密数据的共享学习，论文实现了两个示例合约：

• 基于财务记录的信用评分
• 根据医疗记录预测心脏病的可能性

提供给这些示例合约的训练数据被视为敏感数据，不会在合约外作为明文公开。

智能建筑热力学模型

论文移植了一个非线性最小二乘的实现，用于基于智能建筑提供的时间序列热力学数据来预测温度。Ekiden允许合约运行其模型，同时对传感器数据和模型保密，这表明Ekiden对高度交互的工作负载具有足够的响应能力。

代币

最流行的以太坊合约是ERC20代币标准。论文实现了一个直接用Rust编写的代币合约，Ekiden会自动提供隐私和匿名性，而这是智能合约在以太坊主网上无法实现的。代币中每个用户的帐户余额是保密的。

扑克

论文实现了一个扑克合约，其中用户轮流向合约提交他们的行动，智能合约包含了洗牌和(有选择地)显示牌的所有游戏逻辑。扑克是区块链系统和安全多方计算的通用基准测试应用程序。Ekiden在每次行动后都将保存状态到区块链，并且可以从任何Enclave访问，所以如果玩家中止行动，秘密纸牌仍然能够被显示出来。

加密猫

加密猫是一款以太坊游戏，允许用户繁殖虚拟猫，虚拟猫以ERC721代币的形式存储在链上。每只猫都有一组独特的基因，这些基因决定了它的外观和价值。后代的特征是由一个混合了父母基因的智能合约决定的。基因混合合约的源代码并不公开：游戏开发者的目标是让繁殖过程变得不可预测。

论文从以太坊区块链获取了基因混合合约的字节码，并使用Ekiden EVM端口执行。论文通过从以太坊网络复制真实交易来验证正确性。这个例子展示了Ekiden可以执行以太坊合约，即使源代码不可用。

加密猫的基因混合算法经过了逆向工程，这使得玩家能够优化自己繁殖出具有罕见特征的猫的机会，从而破坏游戏的生态系统。相比之下，Ekiden合约可以访问硬件中的随机性来源，并允许加密存储游戏算法。

Origin

Origin是一个在以太坊之上建立在线市场平台，论文移植了一个demo，允许用户使用Ether列出和购买道具。该应用进一步证明了以太坊的开发框架可以很容易地被Ekiden使用：在demo中使用的智能合约无需修改。基于Ekiden，区块链中的用户交易历史保持隐私，交易确认速度比以太坊更快。

8.评估

与以太坊主网上的ERC20合约相比，Ekiden-BT可以支持吞吐量提高600倍、延迟降低400倍、货币成本降低1000倍的代币合约。虽然论文预计在使用更大规模区块链部署时，会出现一些轻微的性能下降，但性能优化显著降低了区块链速度的影响。

此外，论文证明Ekiden可以有效地支持计算密集型工作，如机器学习应用程序，这在以太坊上是成本高昂的。

端到端延迟

吞吐量

共识对吞吐量的影响

to be continued