古典替换密码
恺撒密码
每个字母用其后的第三个字母替换,即
Plain: ABCDEFGHIJKLMNOPQRSTUVWXYZ
Cipher: DEFGHIJKLMNOPQRSTUVWXYZABC
- 恺撒密码的一般形式,可以将字母移动的位数由3变为1-25中的任何一个
混合单表替换密码
- 每个字母可以用其它任何一个字母替换(不能重复)
- 密钥长度为26个字母,因为每个字母需要一个映射
简单的单表替换密码
- 设置一个没有重复字母的“密钥字”,其它字母按顺序写在密钥字最后字母后面
给定密钥字 JULISCAER
Plain: ABCDEFGHIJKLMNOPQRSTUVWXYZ
Cipher: JULISCAERTVWXYZBDFGHKMNOPQ
多字母替换密码
使用多个单字母替换表,因此一个字母可以被多个字母替换:用一个密钥选择每个字母使用哪个字母表,密钥的第i个字母表示使用第i个字母表,依次使用每个字母表,当密钥的字母使用完后,再从头开始
古典置换密码
- 方法:通过重新编排消息字母隐藏信息
- 特点:没有改变原来消息的字母集
- 关键思想:按一定规则写出明文,按另一规则读出密文
- 密钥:用于读密文的方法和写明文的方法
分组密码
在分组密码中,消息被分成许多块,每块都要被加密
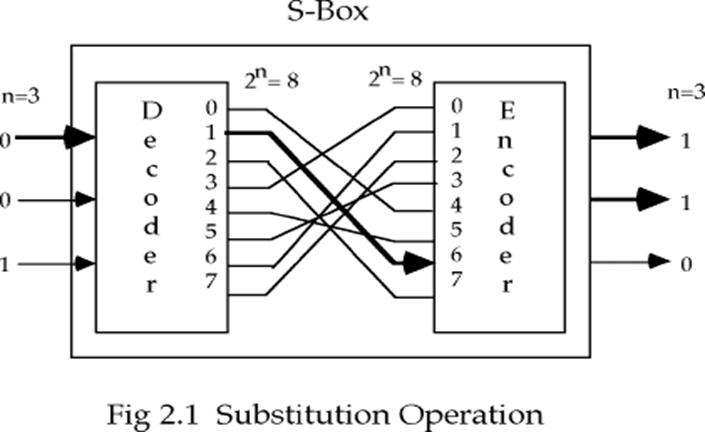
替换运算 S-boxes
-
一个二进制字用其它二进制字替换,这种替换函数就构成密钥,可以看作是一个大的查表运算
-
混淆:使作用于明文的密钥和密文之间的关系复杂化
置换运算 P-boxes
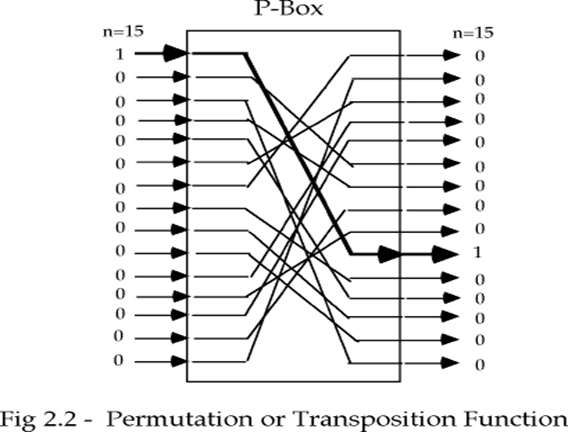
- 二进制字次序被打乱,重新排序的方法构成密钥
- 扩散:将明文及密钥的影响尽可能迅速地散布到较多个输出的密文中
雪崩效应
- 输入改变1bit, 导致近一半的比特发生变化
- 保证小的输入变化导致大的输出变化
完备性效应
- 每个输出比特是所有输入比特的复杂函数的输出
- 保证每个输出比特依赖于所有的输入比特
Feistel密码
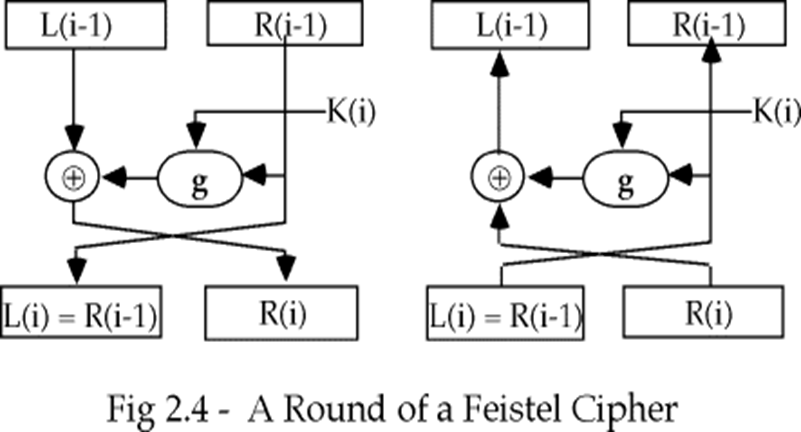
- 把输入块分成左右两部分
- 轮函数g是一个S-P网络
- 由第i个密钥控制(子密钥)
L(i) = R(i-1)
R(i) = L(i-1) xor g(K(i), R(i-1))
- 求逆很容易
- 实际中,一些这样的连续变换形成完整密码变换
Feistel密码设计
- 分组大小:增加分组长度会提高安全性, 但降低了密码运算速度
- 密钥大小:增加密钥长度可以提高安全性(使得穷搜索困难),但降低了密码速度
- 轮数:增加轮数可以提高安全性,但降低速度
- 子密钥生成:子密钥生成越复杂就越安全,但降低速度
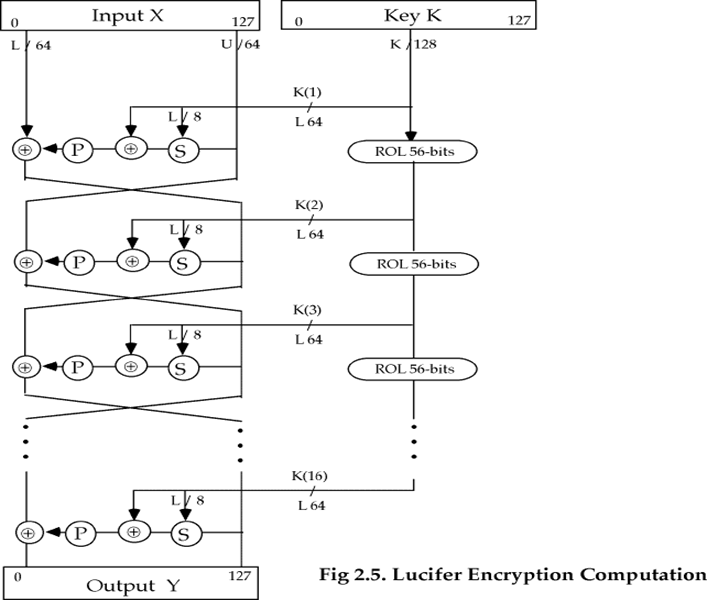
Lucifer
- 分组长度是128-bit,密钥长度是128-bit
- 每轮使用的子密钥是密钥的左半部分
- 密钥每次要向左旋转56-bits,所以密钥的每部分都参加运算
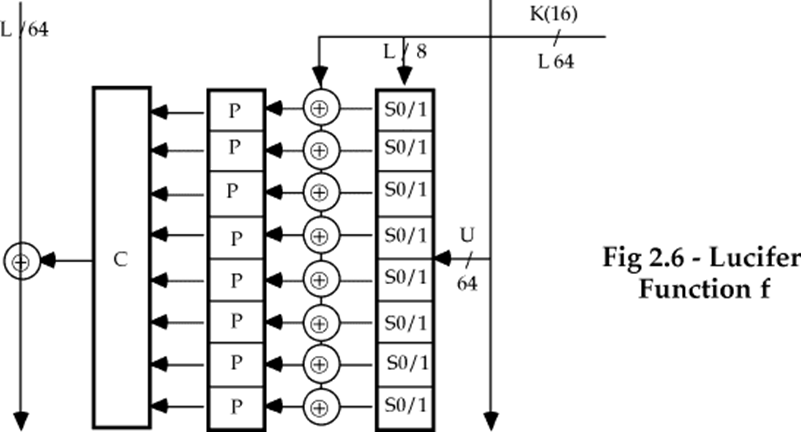
轮函数的具体结构:
现代分组加密算法
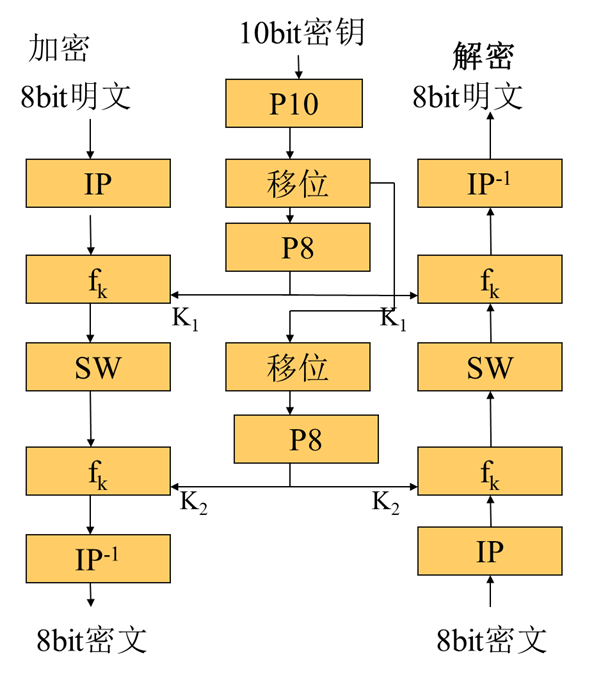
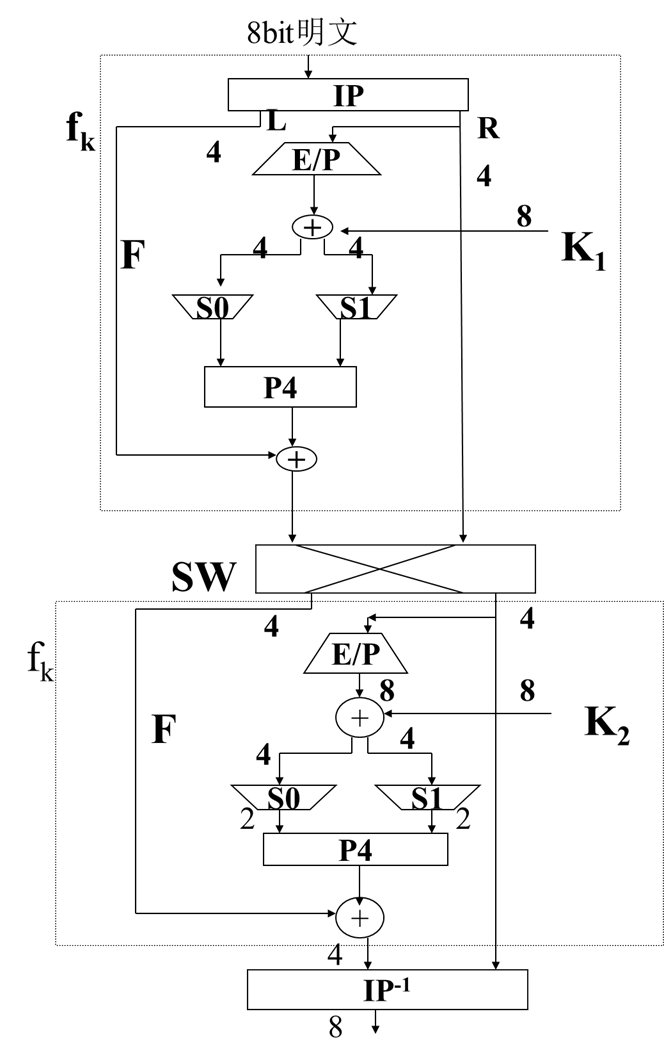
简化的DES (S-DES)
加密算法涉及五个函数:
- 初始置换 IP
- 复合函数 fk1 ,由密钥K确定,具有转换和替换的运算
- 转换函数 SW
- 复合函数 fk2
- 初始置换IP的逆置换 IP-1
加解密流程
-
密文 = IP-1(fk2(SW(fk1(IP(明文)))))
-
明文 = IP-1(fk1(SW(fk2(IP(密文)))))
-
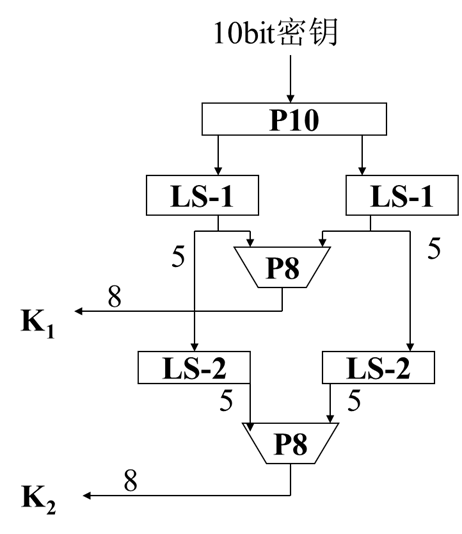
密钥生成:
-
P10(k1, k2, k3, k4, k5, k6, k7, k8, k9, k10) = (k3, k5, k2, k7, k4, k10, k1, k9, k8, k6)
-
P8(k1, k2, k3, k4, k5, k6, k7, k8, k9, k10) = (k6, k3, k7, k4, k8, k5, k10, k9)
-
LS-1为循环左移1位,LS-2为循环左移2位
-
-
IP函数:
IP= 1 2 3 4 5 6 7 8
2 6 3 1 4 8 5 7
IP-1= 1 2 3 4 5 6 7 8
4 1 3 5 7 2 8 6
-
函数fk:fk(L, R) = (L xor F(R, SK), R) , 其中SK为子密钥
-
F是一个4-bit到4-bit的映射:
-
首先对R做扩张/置换(E/P)运算
E/P运算:(1, 2, 3, 4) => (4, 1, 2, 3, 2, 3, 4, 1)
-
将子密钥SK(对应具体算法中的K1和K2)与E/P运算的结果异或得到8-bit数
P0,0 P0,1 P0,2 P0,3
P1,0 P1,1 P1,2 P1,3
-
第一行进入S盒S0,第二行进入S盒S1,分别产生2-bit输出
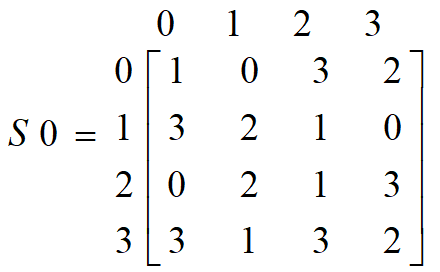
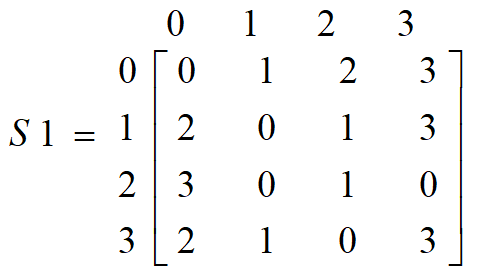
第1和第4输入比特决定行,第2和第3输入比特决定列,以确定选取S-盒元素的位置
如 (P0,0 P0,3)=(0 0),并且(P0,1 P0,2)=(1 0),则选取S盒矩阵的第0行第2列的元素作为2-bit输出
-
-
-
加密具体过程
数据加密标准DES
DES加密流程
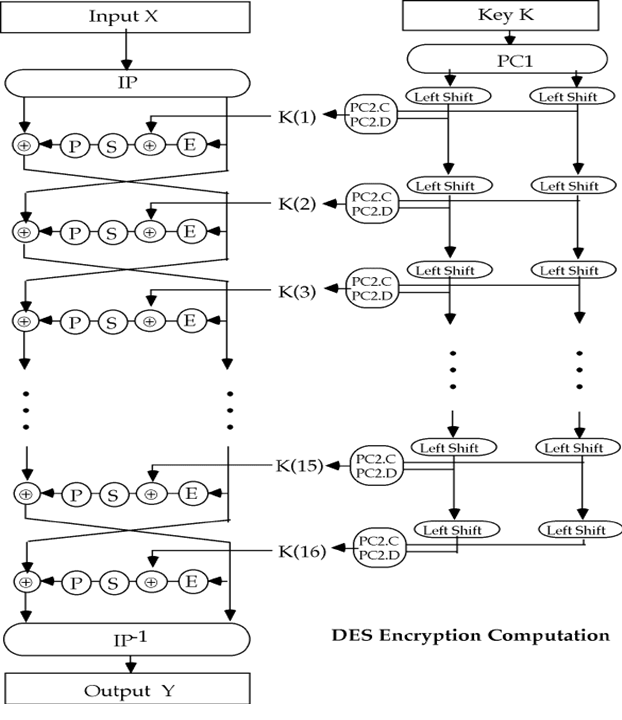
- 对明文X,通过一个固定的初始置换IP得到X0:
X0 = IP(X) = L0R0 , 分为左右两部分。- 函数F的16次迭代:LiRi (1<=i<=16)
Li = Ri-1 , Ri = Li-1 xor F(Ri-1, Ki)
其中Ki是长为48位的子密钥。- 对比特串R16L16使用逆置换IP-1得到密文Y:
Y = IP-1(R16L16)
DES一轮加密
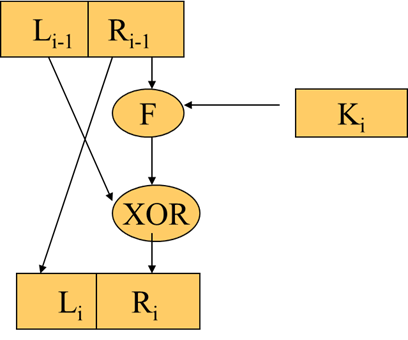
轮函数F
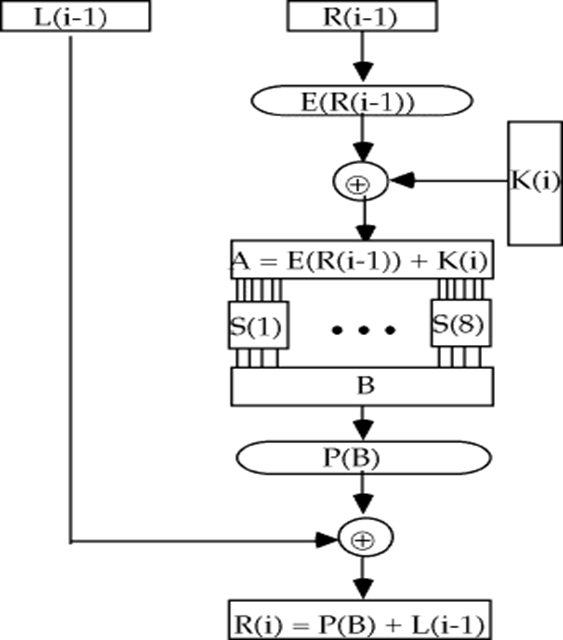
F(Ri-1, Ki) ,输入为32-bit的Ri-1和48-bit的子密钥Ki
- 对Ri-1使用扩展函数E,扩展为48-bit
- 计算 E(Ri-1) xor Ki ,结果写成8个6-bit串 B=b1b2b3b4b5b6
- 使用8个4*16的S盒,其中的元素取0~15的整数,每个S盒输出为4-bit串:
- b1b6确定S盒的行数,b2b3b4b5确定S盒的列数
- 最后,P为固定置换,输出为32-bit串
密钥K计算子密钥
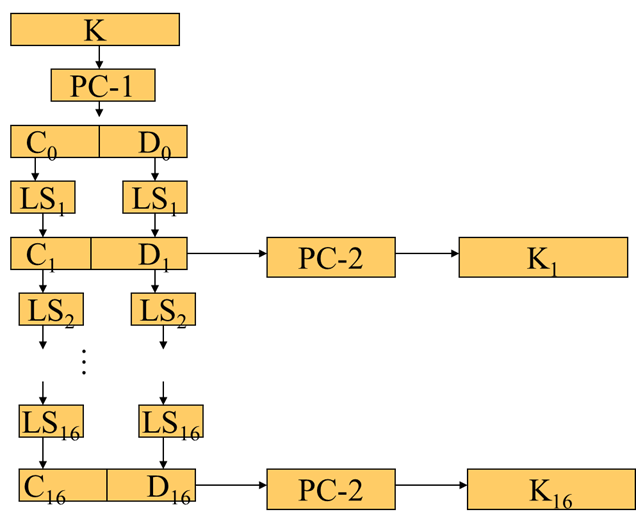
密钥K是长度为64的位串:56位参加子密钥编排,8位是奇偶校验位,在密钥编排的计算中,不参加运算。
给定64位的密钥K,放弃奇偶校验位(8, 16, …, 64),先进行PC-1固定置换,结果为前28-bit的C0和后28-bit的D0
对1 <= i <= 16,计算
Ci = LSi(Ci-1)
Di = LSi(Di-1)
其中LSi表示循环左移1或2位,当i=1,2,9,16时移1位,其他情况移2位
计算 Ki = PC-2(CiDi)
DES的S盒
DES的核心是S盒
- S盒不是它输入变量的线性函数
- 改变S盒的一个输入位至少要引起两位的输出改变
- 对任何一个S盒,如果固定一个输入比特,其它输入变化时,输出数字中0和1的总数近于相等
双重DES
加密:C = EK2[EK1[P]]
解密:P = DK1[DK2[P]]
三重DES
两个密钥加密:C = EK1[DK2[EK1[P]]]
IDEA
- 分组长度为64位,子分组长度为16位
- 密钥长度为128位
- 进行8轮循环
- 同一算法既可以加密也可以解密
IDEA加密总体方案
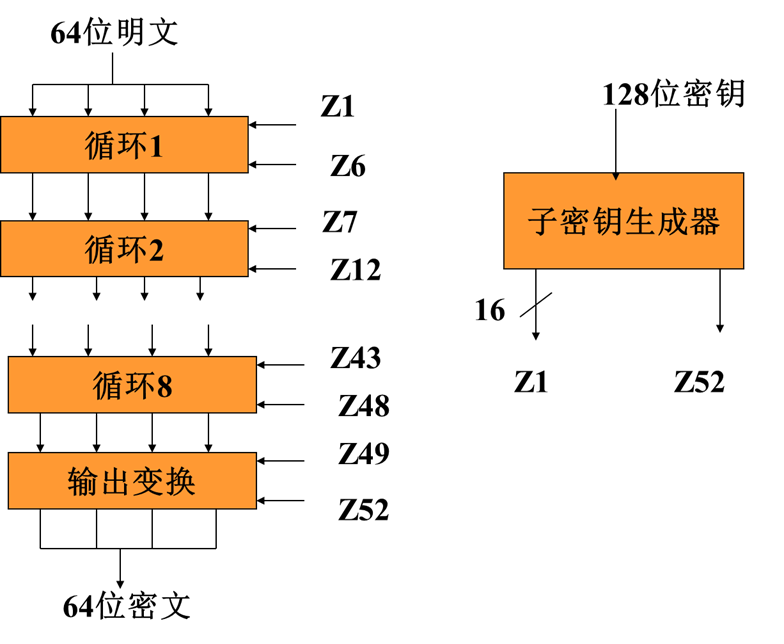
IDEA加密具体过程
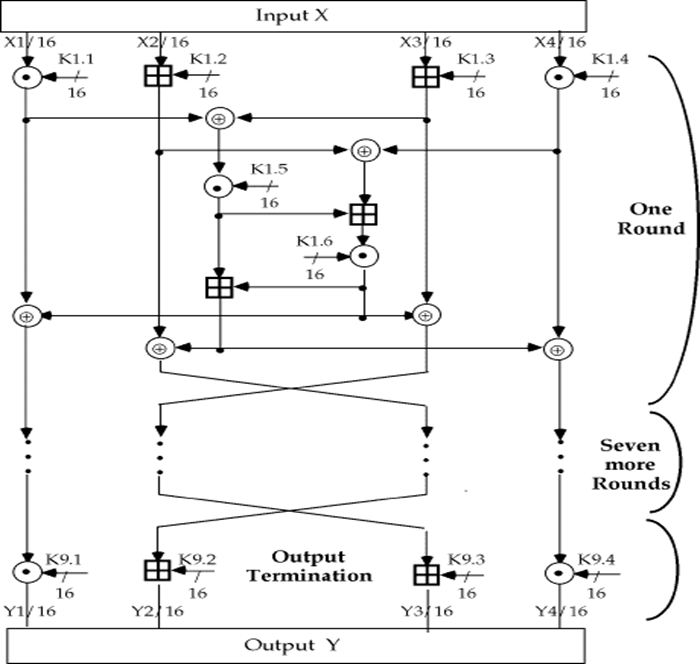
 是整数模216+1乘 (IDEA的S盒)
是整数模216+1乘 (IDEA的S盒) 是整数模216加
是整数模216加
IDEA的密钥生成
52个16-bit的加密子密钥从128-bit的密钥中生成:
- 前8个子密钥直接从密钥中取出;
- 对密钥进行25-bit循环左移,接下来的密钥从中取出;
- 重复进行直到52个子密钥全部生成。
解密密钥从加密子密钥中导出:
- 解密循环 i 的前4个子密钥从加密循环 10-i 的前4个子密钥中导出:
- 解密密钥的第1、4个子密钥对应于1、4加密子密钥的乘法逆元;
- 解密密钥的第2、3个子密钥对应于2、3加密子密钥的加法逆元
- 对前8个循环来说,循环 i 的最后两个子密钥等于加密循环 9-i 的最后两个子密钥
AES-Rijndael
- 可变块长、可变密钥长度
- 分组长度指定为128位
- 密钥长度为128,192或256位,相应的迭代轮数为10、12和14
AES框架
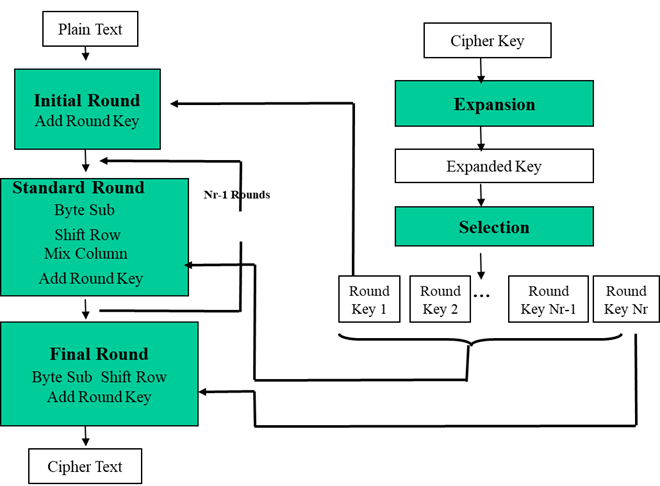
AES轮函数
每一轮迭代的结构都一样,只是最后一轮省略了列混合变换:
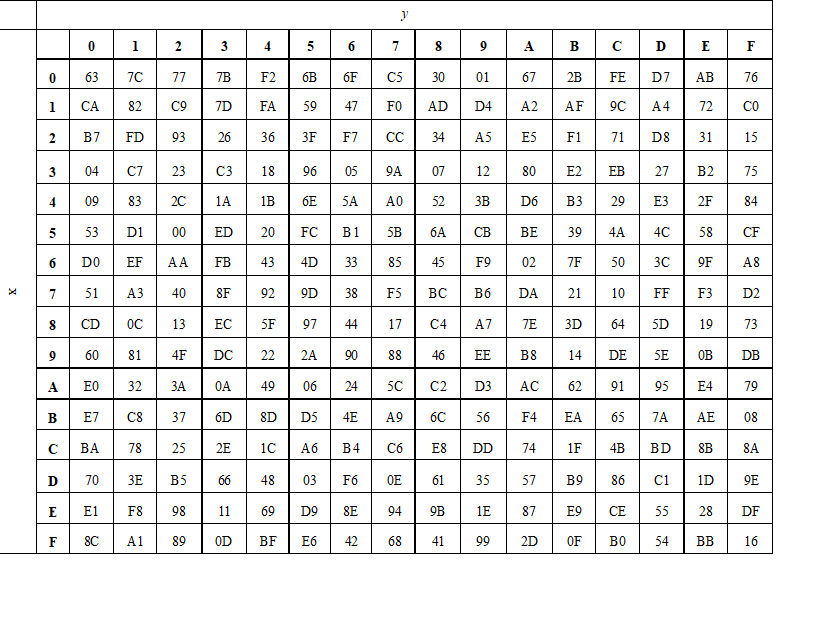
字节替换(Byte Sub)
对数据的每一字节应用一个非线性变换;
替换表是一个16×16的矩阵。表中纵向的x取自状态矩阵中的高4比特,横向的y取自低4比特。
行移位(Shift Row)
对每一行的字节循环重新排序,可以表示为: Bi,j = Ai,(i+j)mod4
列混合(Mix Column)
对矩阵的列应用一个线性变换:
- 将状态的每一列视为GF(28)上的多项式S(x),然后乘以固定多项式a(x),并模除x4+1。其中a(x) = {03}x3+{01}x2+{01}x+{02}
- a(x)存在关于x4+1的逆元,变换的矩阵为:

- 列混合变换的结果为:

轮密钥加(Add Round Key)
-
把轮密钥混合到中间数据,对状态和每轮的子密钥进行简单的异或操作
-
每轮子密钥是通过密钥调度算法从主密钥中产生,子密钥长度等于分组长度
-
轮密钥加运算需要用到4个导出的32比特子密钥
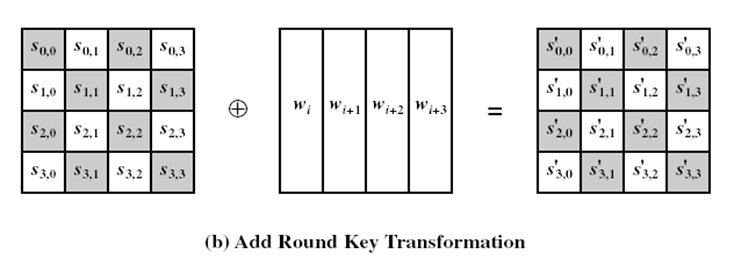
AES子密钥生成
Rijindael算法每一轮需要用到Nb比特的子密钥,共有Nr轮,另外,第一次轮密钥加的时候也需要用一轮子密钥,于是总共需要Nb*(Nr+1)比特的子密钥,对于AES-128来说就是用1408比特的子密钥
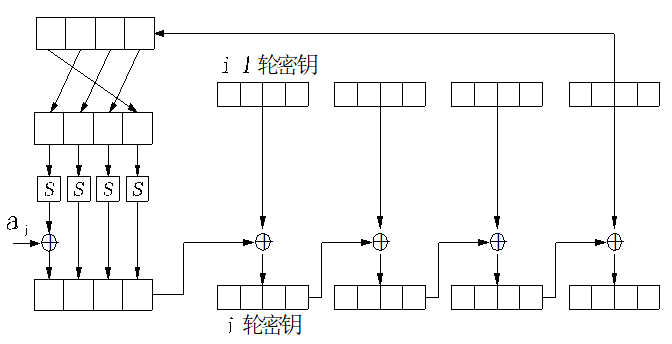
AES解密过程
逆字节替换、逆行移位、逆列混合、轮密钥加(其逆变换就是本身)
分组密码工作模式
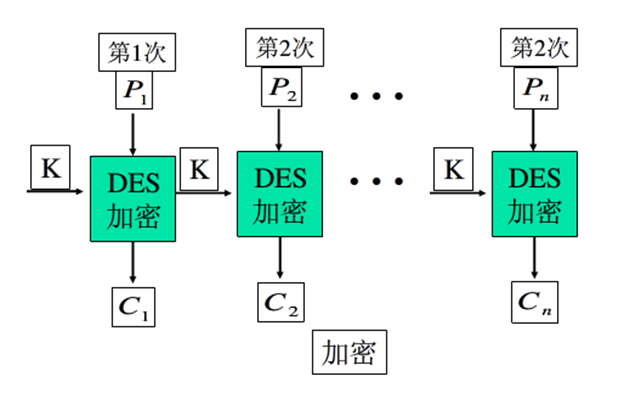
ECB 电码本模式
- 消息分成相互独立的加密模块
- 每块独立使用DES算法
- 适合少量的数据加密
- 如果最后一个分组长度不够,需要填充
- 对于同一个明文分组,如果出现多次,其密文是相同的,因为每次的加密密钥都相同 (缺陷)
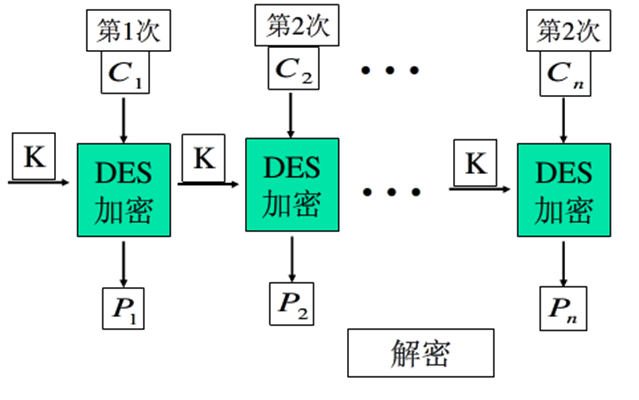
CBC 密码分组链接模式
- 使重复的明文分组产生不同的密文分组:每次加密使用相同加密密钥,但是输入是当前明文分组盒前一个密文分组的异或
- 适合加密长度大于64比特的消息
- 如果最后一个分组长度不够,需要填充
- 可以用来进行用户鉴别
- 错误传播
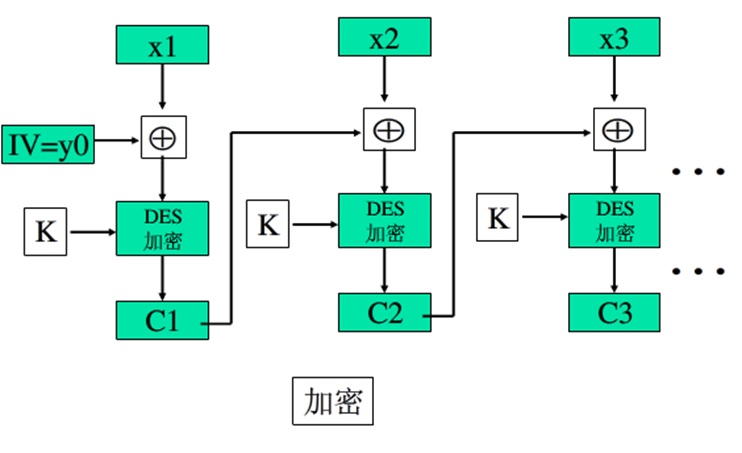
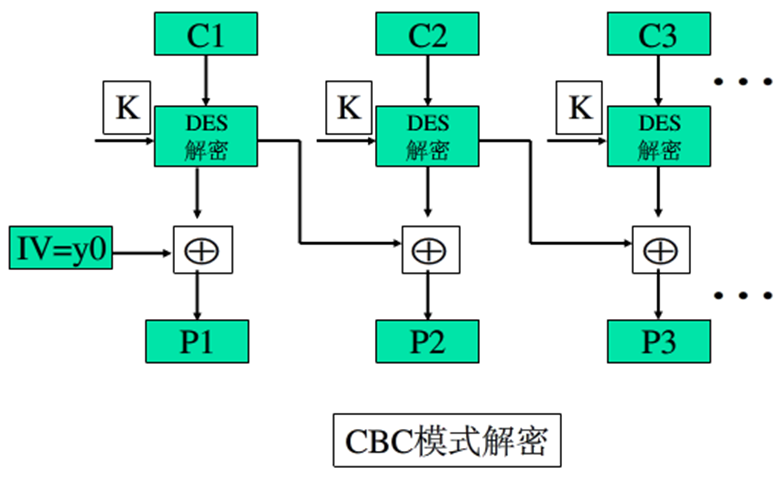
- 解密时,每一个密文分组被解密后,再与前一个密文分组异或,便能得到明文分组
- 产生第一个密文分组时,需要一个初始向量IV与第一个明文分组异或,IV对于收发方都是已知的,且应该像密钥一样被保护
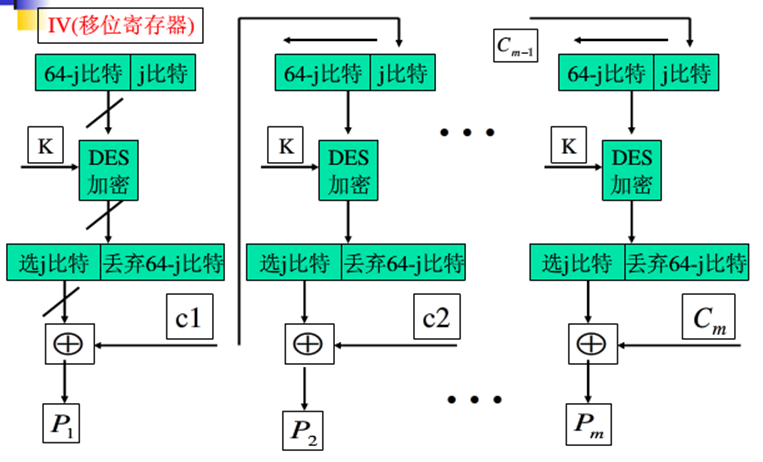
CFB 密码反馈模式
- 消息作为比特流,不需要对消息填充
- 适合数据以比特或字节为单位出现
- 错误传播
- 可以用于认证
加密过程:
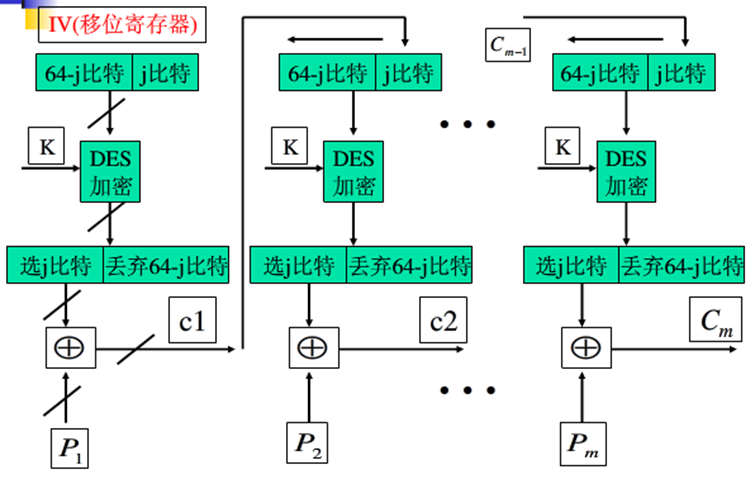
解密过程:
- 将收到的密文单元和加密函数的输出进行异或
- 仍然使用加密算法而不是解密算法
OFB 输出反馈模式
- 结构类似CFB,不同之处在于OFB将加密算法的输出反馈到移位寄存器,而CFB将密文单元反馈到移位寄存器
- 消息作为比特流,不需要对消息填充
- 比特错误不会被传播
加密过程:
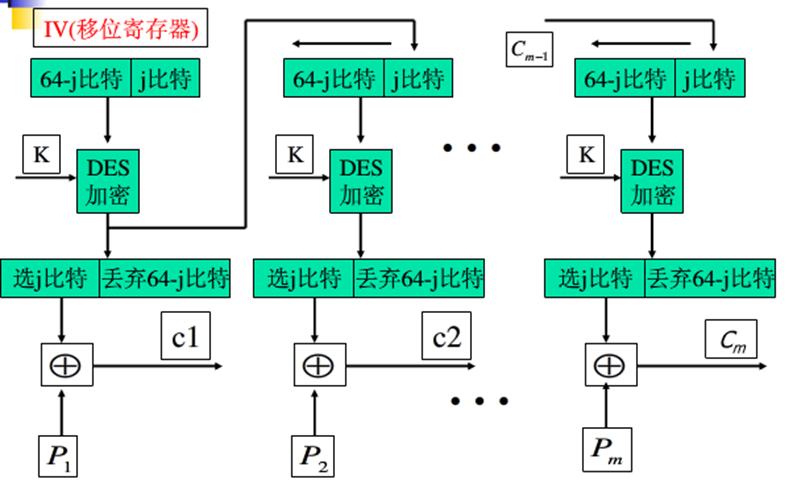
解密过程:
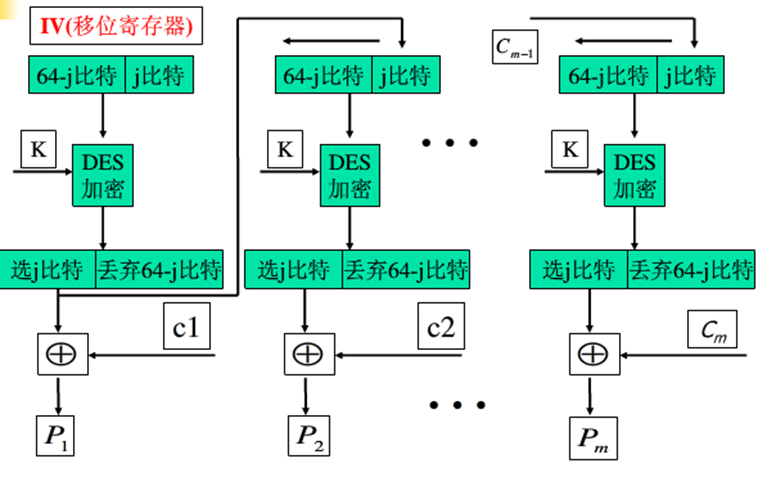
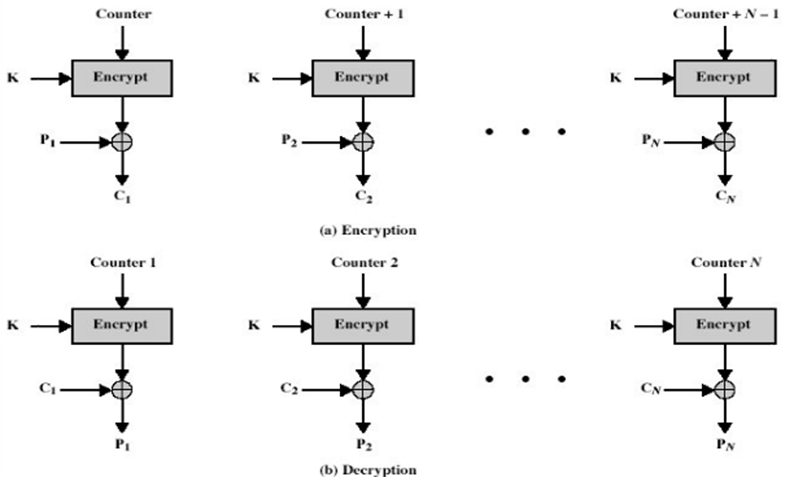
CTR 计算器模式
- 可并行加密
- 预处理
- 吞吐量仅受可使用并行数量的限制
- 加密数据块随机访问
流密码
流密码简单结构
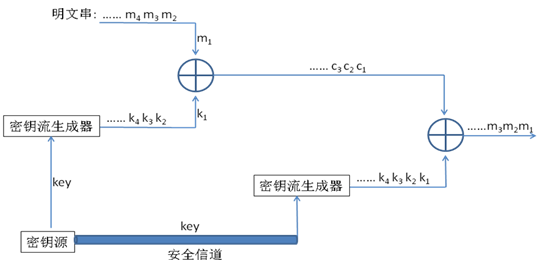
- 密钥源是一个容易记住的密钥
- 密钥流生成器生成一个周期较长、可用于加解密运算的伪随机序列
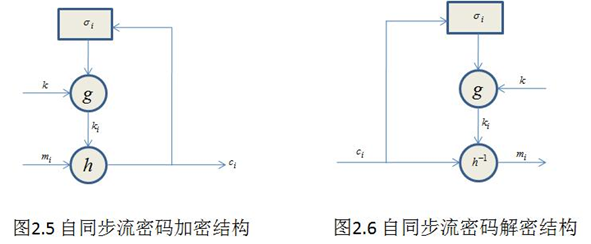
同步流密码与自同步流密码
同步流密码
- 密钥流的产生与明文消息流相互独立
- 无错误传播:在传输期间一个密文字符被改变只影响该符号的恢复,不会对后继的符号产生影响
自同步流密码
密钥流的产生与之前已经产生的若干密文有关
线性反馈移位寄存器 LFSR
- 用于生成密钥流:
- LFSR的结构非常适合硬件实现
- LFSR的结构便于使用代数方法进行理论分析
- 产生的序列的周期可以很大
- 产生的序列具有良好的统计特性
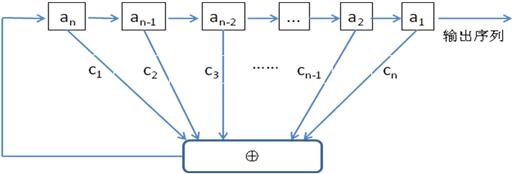
-
反馈函数为:
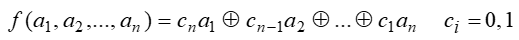 , 其中加法运算为模2加,乘法为普通乘法
, 其中加法运算为模2加,乘法为普通乘法 -
第t+1时刻第i级寄存器的内容为:
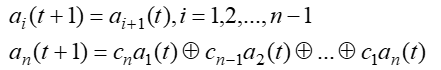
-
LFSR的联接多项式为:
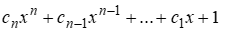
LFSR的周期与m序列
- 一个n级LFSR序列的周期最大只能是2n-1
- 若n级LFSR产生的非零序列的周期为2n-1,则称其为m序列
- 一个n级LFSR为最长移位寄存器的充要条件是它的联接多项式为F2上的n次本原多项式
- 2n-1为素数时,F2上的每一个n次不可约多项式均为n次本原多项式
伪随机序列
Golomb随机性假设

注:游程指一段连续的相同数字
m序列的伪随机性

线性复杂度
线性复杂度:能够输出该序列的最小线性移位寄存器的级数,即次数最小的联接多项式
- 如果序列的线性复杂度为l(>=1),则只要知道序列中任意相继的2l位,就可确定整个序列
安全的密钥流
- 周期充分长,一般不少于1016
- 随机统计特性好,即基本满足Golomb的随机性假设
- 大的线性复杂度,为序列长度的一半
基于LFSR的伪随机序列生成器
在LFSR的基础上加入非线性化的手段,产生适合于流密码应用的密钥序列(伪随机序列)
滤波生成器
由一个n级线性移位寄存器和一个m(<n)元非线性滤波函数组成,滤波函数的输出为密钥流序列
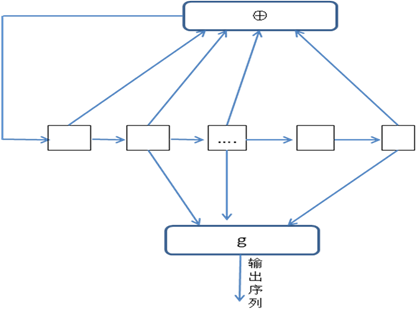
- g是一个m元布尔函数
组合生成器
若干个线性移位寄存器LFSRi(i=1, …, n)和一个非线性组合函数组成,组合函数的输出构成密钥流序列
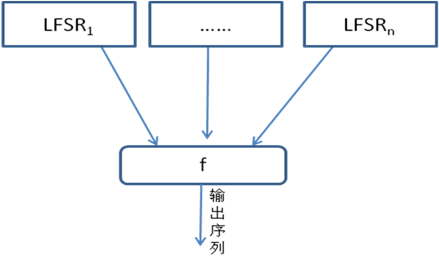
- 其中LFSRi为n个级数分别为r1, r2, …, rn的线性移位寄存器
- f是n元布尔函数
钟控制生成器
用一个或多个移位寄存器来控制另一个或多个移位寄存器的时钟
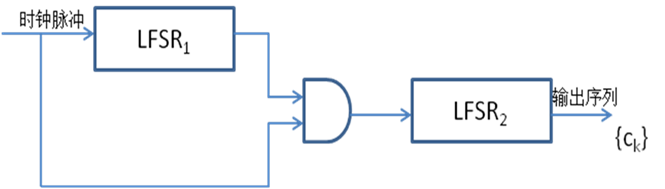
- 当LFSR1输出1时,移位时钟脉冲通过与门使LFSR2进行一次移位,从而生成下一位
- 当LFSR1输出0时,移位时钟脉冲无法通过与门影响LFSR2,因此LFSR2重复输出前一位
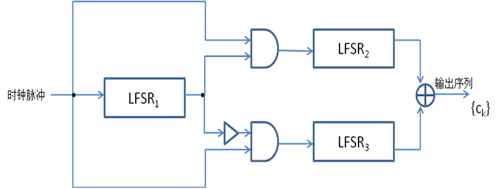
- 当LFSR1的输出是1时,LFSR2被时钟驱动
- 当LFSR1的输出是0时,LFSR3被时钟驱动
- LFSR1的输出与LFSR2的输出做异或运算即为这个交错式停走生成器的输出
实用流密码
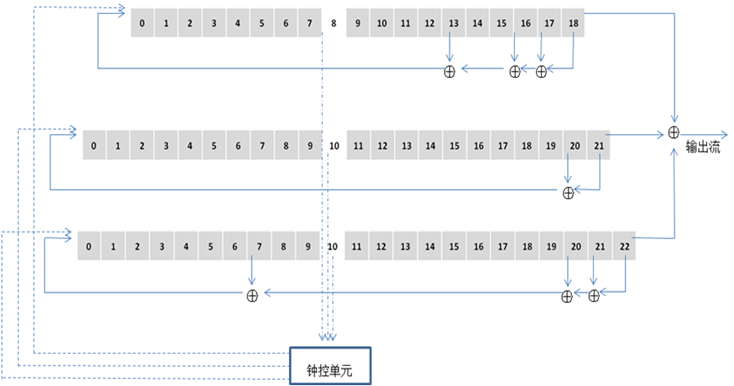
全球移动通信系统GSM中的A5算法
A5的钟控机制:如果在某一时刻钟控单元中三个值的某两个或三个相同,则对应的移位寄存器在下一时刻被驱动,而剩下的一个(或0个)值对应的移位寄存器则停走
RC4
- 参数n,长为n的秘密内部状态(2n数组),当n取8时,内部状态有256(=2n)个元素(S[0], S[1], …, S[255])构成,每个元素都是0~255之间的一个数字
- 输入:一个可变长的密钥,用于初始化内部状态
- 输出:状态中按照一定方式选出的某一个元素K,该输出构成密钥流的一个字节,加解密时,K与一个明文/密文字节执行XOR运算
- 每生成一个K值,内部状态中的元素会被重新置换一次,以便下次生成K值
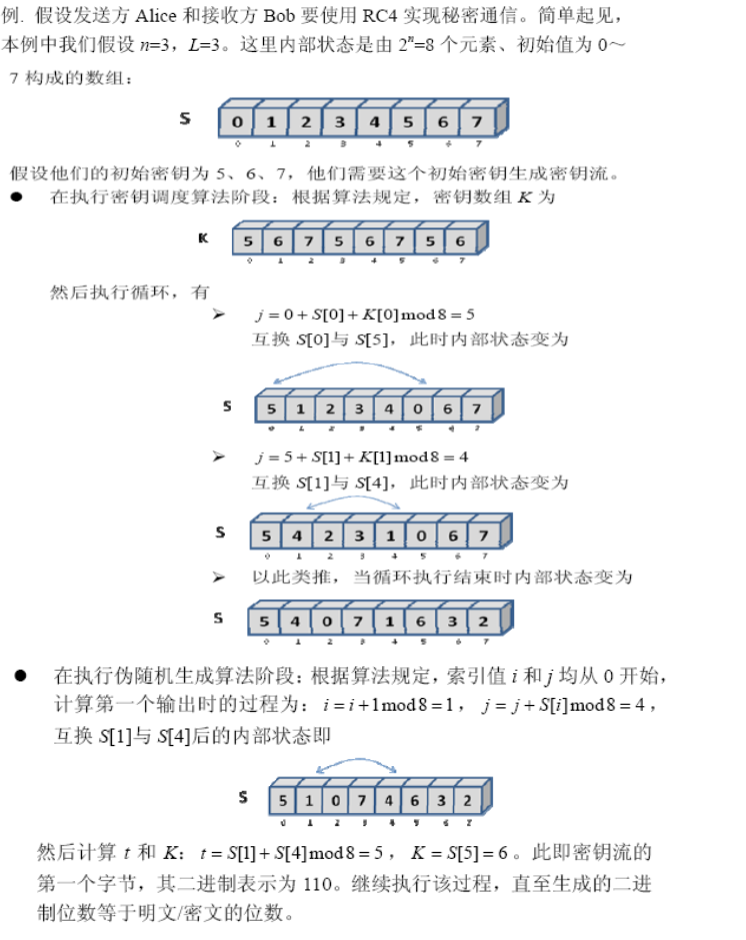
密钥调度算法
-
用来设置内部状态的随机排列,最开始设置为S[i]=i (i=0, 1, …, 255)
-
密钥长度可变,设为L个字节(K[0],…, K[L-1]),一般L在5~32之间,用这L个字节不断重复填充,直到得到 K[0],…, K[255]。该数组K将被用于对内部状态S进行随机化

伪随机生成算法
从内部状态中选取一个随机元素作为密钥流中的一个字节,并修改内部状态以便下一次选取

例子
公钥密码
对称密码体制的缺陷
- 密钥分配问题:缺少安全信道
- 密钥管理问题:任意两个用户之间都需要共享密钥,数量级很大
- 没有签名功能
公钥算法分类
- Public Key Distribution Schemes (PKDS) 密钥交换
- 用于交换秘密信息(依赖于双方主体)
- 常用于交换对称加密算法的密钥
- Public Key Encryption (PKE) 公钥加密
- 用于加密任何消息
- 任何人可以用公钥加密消息
- 私钥的拥有者可以解密消息
- 任何公钥加密方案能够用于密钥分配方案PKDS
- 许多公钥加密方案也是数字签名方案
- Signature Schemes
- 用于生成对某消息的数字签名
- 私钥的拥有者生成数字签名
- 任何人可以用公钥验证签名
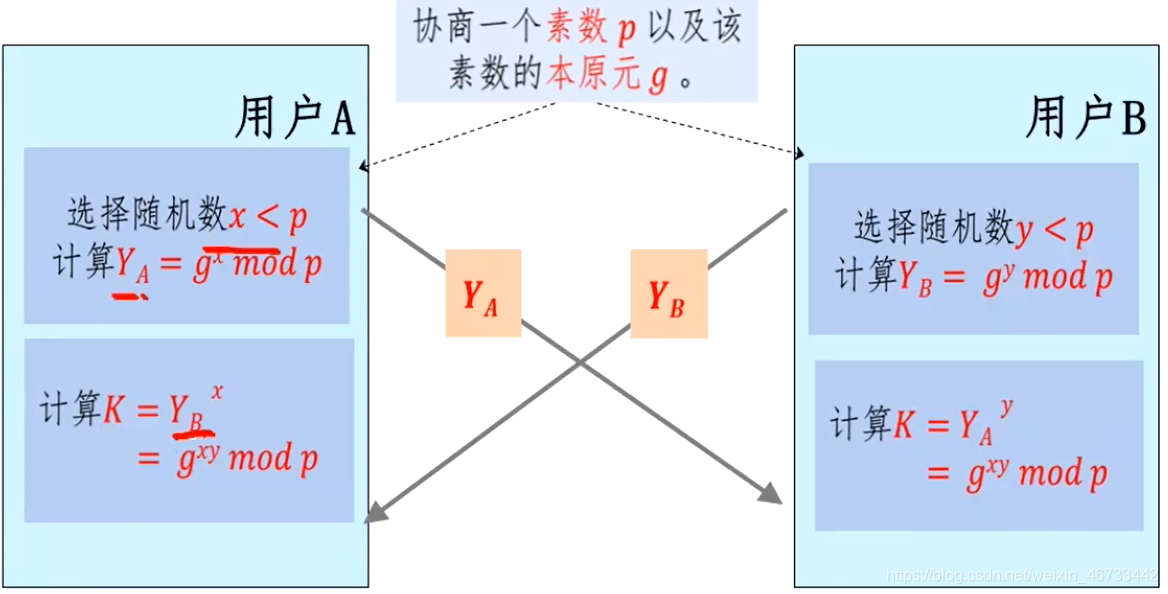
Diffie-Hellman密钥分配
- 不能用于交换任意消息
- 基于有限域上的指数问题
- 安全性是基于计算离散对数的困难性
- 能抵抗被动攻击,不能抵抗主动攻击(中间人)
RSA
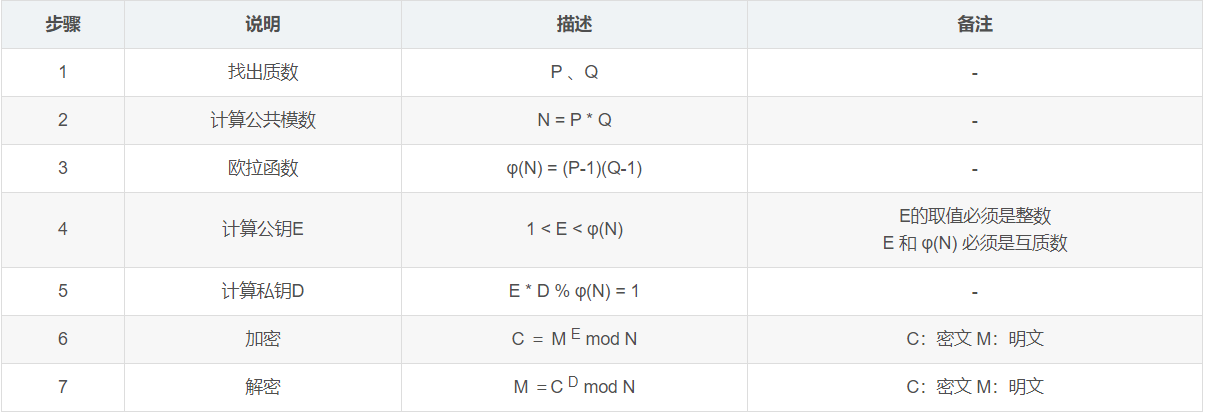
- 素数p, q要求足够大
- 通常选择小的加密指数E,可以对所有用户都相同
RSA快速实现
- 加密快,指数小;解密慢,指数大
- 利用中国剩余定理CRT快速实现RSA解密(M=CD mod N):
- M1 = M mod p = (C mod p)Dmod(p-1)
- M2 = M mod q = (C mod q)Dmod(q-1)
- 解方程:M = M1 mod p 和 M = M2 mod q
- 具有唯一解(利用CRT):M = (quM1 + pu’M2) mod N,其中pu mod q =1,qu’ mod p = 1
RABIN公钥密码体制
- 基于二次剩余问题和模n平方根问题
- 加密密钥为2,安全性等价于对大整数n的分解;解密更为困难
- 不能抵抗选择密文攻击
EI Gamal公钥加密
-
D-H算法的变形,用于安全交换密钥
-
安全性基于离散对数
-
缺点:增加消息长度(2倍)

认证和哈希函数
- 认证的主要目的:
- 实体认证(发送者非冒充)
- 消息认证(验证信息的完整性)
- 三类产生认证符的函数:
- 消息加密
- 消息认证码(MAC)
- 哈希函数
消息加密
- 对称加密:提供保密与一定程度的认证,不提供签名
- 公钥加密:(A -> B)
- E(KUb, M) => 提供保密,不提供认证
- E(KRa, M) => 提供认证和签名
- E(KUb, E(KRa, M)) => 提供保密、认证和签名
消息认证码(MAC)
对选定消息使用一个密钥产生一个短小的定长数据分组,附加在消息中提供认证功能 (MAC = Ck(M))
-
基本用法:
- M || Ck(M) => 提供认证
- Ek2(M || Ck1(M)) => 提供认证(K1)和保密(K2)
- Ek2(M) || Ck1(Ek2(M)) => 提供认证(K1)和保密(K2)
-
适用于消息广播、比消息加密的工作量小、认证与保密分离、延长消息的保护期限
-
不可逆,且不提供数字签名
哈希函数
- 基本用法:
- Ek(M || H(M)) => 提供保密和鉴别
- M || Ek(H(M)) => 提供鉴别
- M || EKRa(H(M)) => 提供鉴别和数字签名
- Ek(M || EKRa(H(M))) => 提供鉴别、数字签名以及保密
- M || H(M || S) => 提供鉴别(S是通信双方共享的一个秘密值)
- Ek(M || H(M || S)) => 提供鉴别和保密
- 哈希函数要求:
- 消息长度任意,输出定长
- 易于计算
- 单向性
- 弱抗碰撞性:任意给定分组x,寻求不等于x的y,使得H(y)= H(x)在计算上不可行
- 强抗碰撞性:寻求对任何的(x,y)对使得H(x)=H(y)在计算上不可行
简单的异或哈希函数
每个n比特长度分组按比特异或,得到长度为n的哈希码
- 改进:(使得输入数据完全随机化,掩盖输入的数据格式)
- 先将n比特的哈希值设置为0
- 当前的哈希值循环左移一位
- 数据分组与哈希值异或形成新的哈希值
- Merkle-Damgard结构:

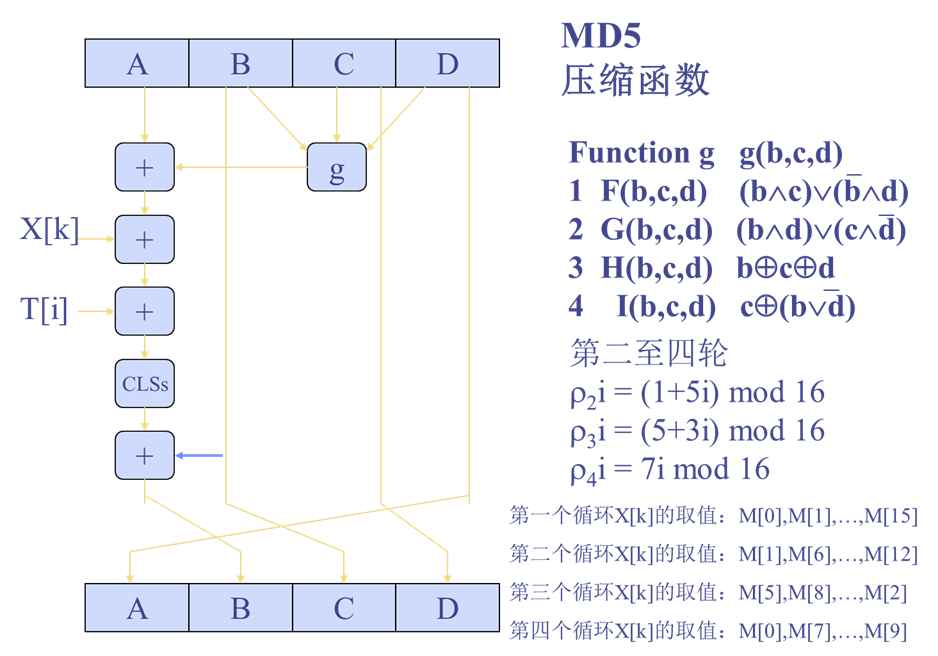
MD5
输入任意长度报文,输出128比特的摘要;输入分组长度为512比特;符合Merkle-Damgard结构
算法流程
-
在消息的最后添加填充位(一个1和若干个0),使得数据的长度满足length = 448 mod 512,填充完后,信息的长度为N*512+448(bit)
-
记录信息长度,用64位来存储填充前信息长度,如果信息长度超过264位,则只保留低64位。这64位加在第一步结果的后面,这样信息长度就变为(N+1)*512(bit)
-
初始化MD缓存,使用一个128位缓存存放哈希的中间和最后结果,缓存表示为4个32位的缓存器(A,B,C,D),初始化格式为低位字节存放在高地址字节
-
四轮循环处理512bit分组
-
输入:当前处理的512位分组Yq与上一轮输出CVq
-
循环:4轮循环依次记为F,G,H,I;借助列表T[1,…,64](T[i]=232 * |sin(i)|的整数部分),列表提供随机化的32位模板以消除输入的规律
-
每个循环包括16步操作,每一步的基本形式:
$$
b \leftarrow b + ((a + g(b, c, d) + X[k] + T[i]) <<< s)
$$- +:模232加
- a, b, c, d:MD缓存中的4个字,一开始被初始化,之后每一步操作结果都会替换其中一个字
- <<< s:循环左移s位
- T[i]:矩阵T中的第i个32比特字,i = 1,…,16
- g:循环函数F、G、H、I
- X[k]:当前分组的第k个字
-
-
输出:第4次循环输出加到第1轮循环的输入上产生CVq+1,相加是缓存中的4个字分别与CVq中对应的4个字以模232相加
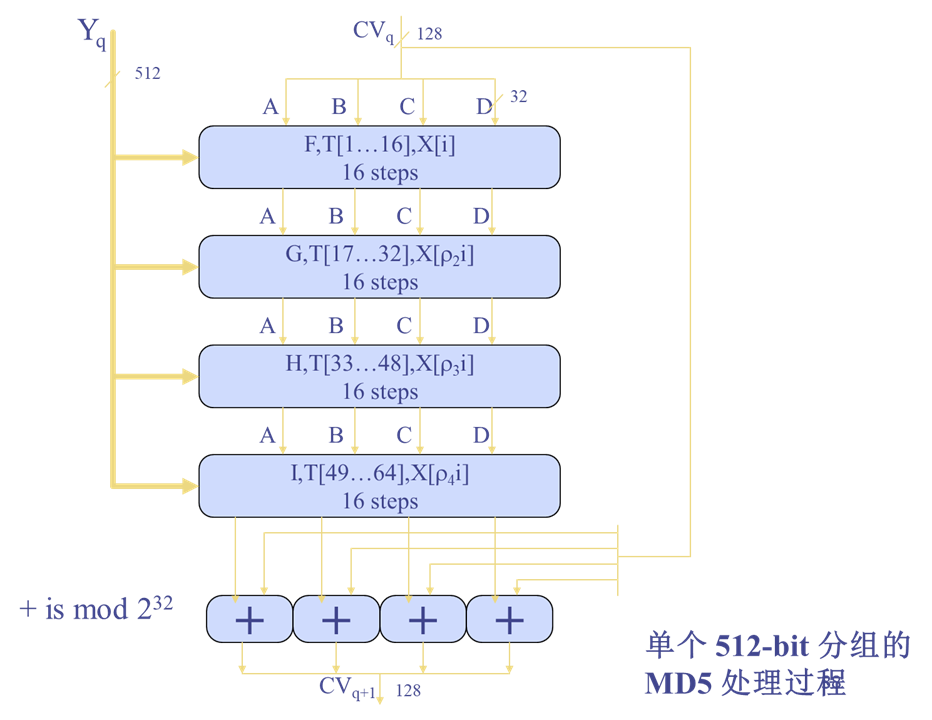
-
MD5应用
- 对明文消息生成消息摘要
- 用于数字签名(UNIX、Linux等操作系统保护用户口令)
MD5口令逆向
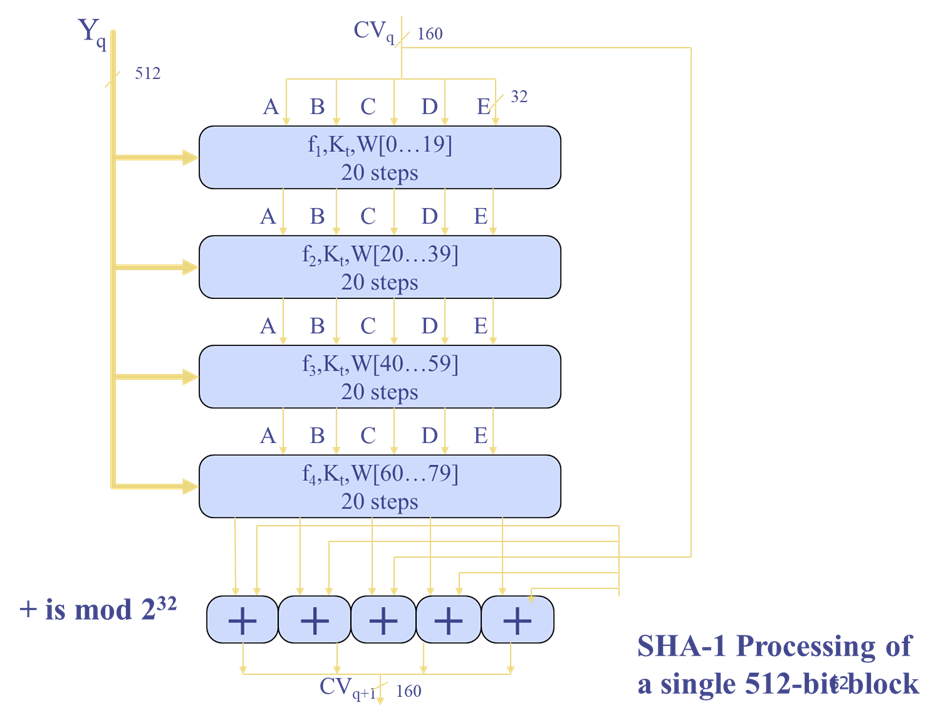
SHA-1
输入最大长度为264位的消息,输出160比特 ,分组为512比特
算法流程
-
在消息的最后添加填充位(一个1和若干个0),使得数据的长度满足length = 448 mod 512,填充完后,信息的长度为N*512+448(bit)
-
记录信息长度,用64位来存储填充前信息长度,如果信息长度超过264位,则只保留低64位。这64位加在第一步结果的后面,这样信息长度就变为(N+1)*512(bit)
-
初始化MD缓冲区,使用160位MD缓冲区来保存中间和最终哈希结果,表示为5个32位寄存器(A,B,C,D,E),存储为低位字节放在低地址字节上
-
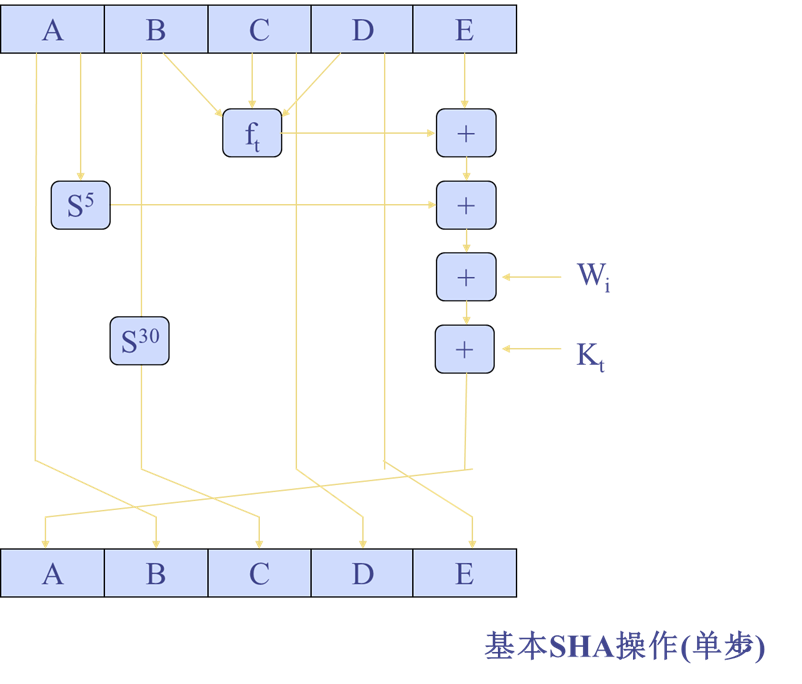
以512位数据块为单位处理消息,4轮,每轮20步,每次循环分别使用一个额外的常数Kt
-
每一步的基本形式:
$$
A,B,C,D,E\leftarrow (E+f_t(B,C,D)+S5(A)+W_i+K_t),A,S{30}(B),C,D
$$-
+:模232加法
-
ft:逻辑函数,每轮循环不同
-
Si:32位常数循环左移i位
-
Kt:额外的常数
-
Wi:当前512位数据导出的一个32位字;共80个
-
前16个直接来自当前分组的16个字
-
其余:
$$
W_t=S^1(W_{t-16}\bigoplus W_{t-14}\bigoplus W_{t-8}\bigoplus W_{t-3})
$$
-
-
-
- 第4次循环输出加到CVq,得到160位CVq+1(模232加)
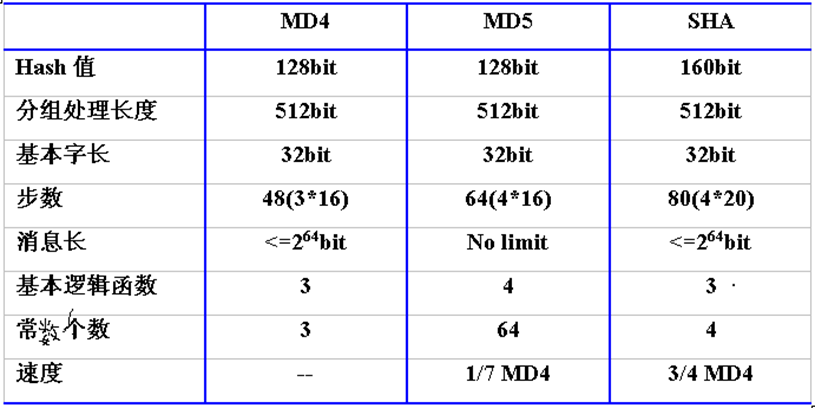
哈希函数对比
- SHA = MD4 + 扩展变换 + 外加一轮 + 更好的雪崩
- MD5 = MD4 + 改进的比特杂凑 + 外加一轮 + 更好的雪崩
数字签名算法
只对消息的哈希签名,否则交换信息长度增加一倍;数字签名可以提供消息的不可否认性
RSA
给定(e, R), (d, p, q)
- 计算明文M的哈希h,S = hd(mod R),发送(M, S)
- 接收方同样计算哈希h,Se mod R = h’ mod R,对比h和h’
- 若先加密后签名,签名可能被替换
EI Gamal
- 加密算法不可交换——需要专门的签名算法
- 安全性基于离散对数的计算困难性
- 公钥:(y, g, p),私钥(x)
- 签名方案:
- 随机数k,与p-1互素
- 计算K = gk mod p
- 计算S = k−1(M − Kx) mod (p−1)
- 发送签名(M, K, S),销毁k
- 验证yKKS mod p=gM mod p
- 签名长度为消息的两倍
DSA
- El Gamal的变形,生成320位签名
- 安全性基于离散对数的计算困难性
- 密钥生成
- 公开参数 (p, q, g)
- p:大素数,2L,L为512到1024位且为64的倍数
- q:160位(p-1)的素因子
- g:h(p−1)/q, h < p−1 且 h(p−1)/q(mod p) > 1
- 选择私钥x,计算y = gx mod p,公钥为 (p, q, g, y)
- 公开参数 (p, q, g)
- 签名生成(SHA:哈希函数)
- r = (gk mod p) mod q
- s = k−1(SHA(M) + xr) mod q
- 发送 (M, r, s)
- 签名验证
- w = s−1 mod q
- u1 = SHA(M)w mod q
- u2 = rw mod q
- v = (gu1yu2 mod p) mod q
- 验证 v = r
HMAC
- 以上为需要私钥的认证方案,计算量大
- 密钥与消息同时参加运算:KeyedHash = Hash(Key | Message)或Hash(Key1 | Hash(Key2 | Message))
- HMAC:使用带密钥hash函数的结果
- HMACK = Hash((K′ ⨁ opad) || Hash((K′ ⨁ ipad) || M))
- K’:经过填充的密钥
- opad、ipad:特殊的填充值
- 安全性基于原始的hash
信息隐藏与隐写分析
信息隐藏的基本概念
信息隐藏是将信息秘密嵌入在数字图像、声音、文档、视频等数字产品中,用以隐蔽通信、隐蔽标识,或识别所有者、完整性、发源地、使用权、序列号等。
信息隐藏技术的主要分支
- 隐蔽信道:系统存在的一些安全漏洞,通过某些非正常的访问控制操作,能形成隐秘数据流,而基于正常安全机制的软硬件不能觉察和有效控制
- 匿名通信
- 源重写技术:采用路由转发策略,发送者匿名
- 隐写术
- 版权标志
水印的分类
根据应用分类:
- 隐蔽通信
- 版权保护
- 认证和完整性
- 内容标注
根据嵌入域分类:
- 空域,如LSB
- 变换域,如DFT、DCT、DWT等
根据是否可见分类
- 可见水印
- 不可见水印
根据密钥分类
- 密钥水印
- 公钥水印
根据原始数据分类
- 私有水印:检测时需要原始数据
- 盲水印:检测时不需要原始数据
根据载体恢复分类
- 可逆水印
- 不可逆水印
根据鲁棒性分类
- 鲁棒水印:用于认证、版权保护
- 半易碎水印
- 易碎水印:对恶意改动敏感,用于完整性判定
鲁棒水印特性
- 不可见性
- 安全可靠性
- 鲁棒性
- 复杂性
- 容量
信息隐藏的一般过程
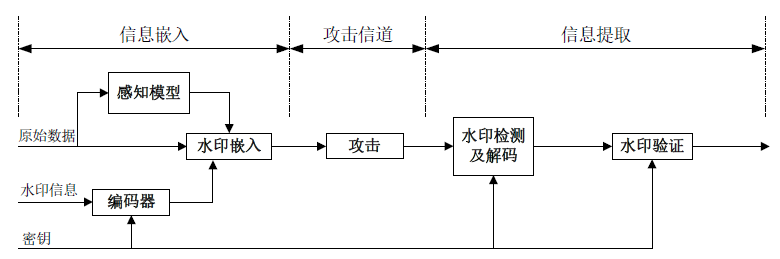
水印生成
类似噪声,具有不可预测的随机性
- Arnold置乱技术:置乱96次回到原图
- 扩频技术
- 基于片率
- 基于伪随机序列
水印嵌入
- 加法嵌入:Xw(k) = X0(k) + a(k)w(k)
- 乘法嵌入:Xw(k) = X0(k)(1 + a(k)w(k))
信息隐藏的常见算法
空域信息隐藏算法
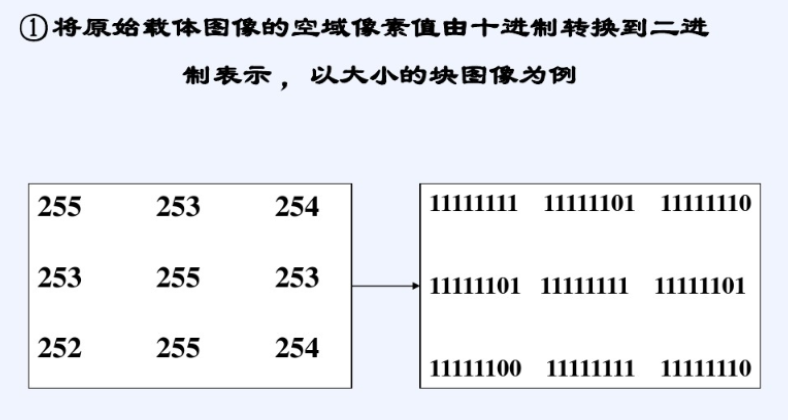
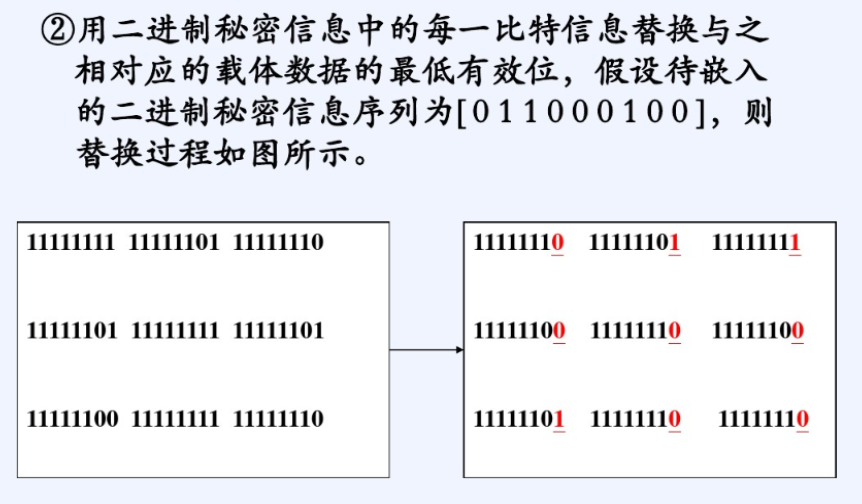
通过直接修改像素值实现信息嵌入
- 优点:简单、快速、容量大
- 缺点:鲁棒性差
图像位平面特性:
- 位平面越高,对灰度值的贡献越大,相邻比特的相关也越强
- 最低位平面类似随机噪声
LSB算法

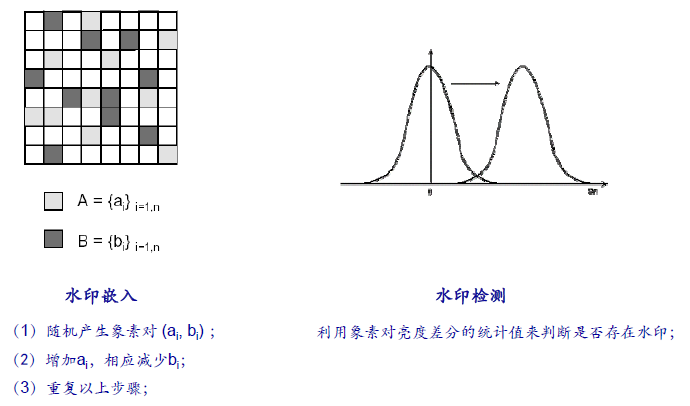
Patchwork算法
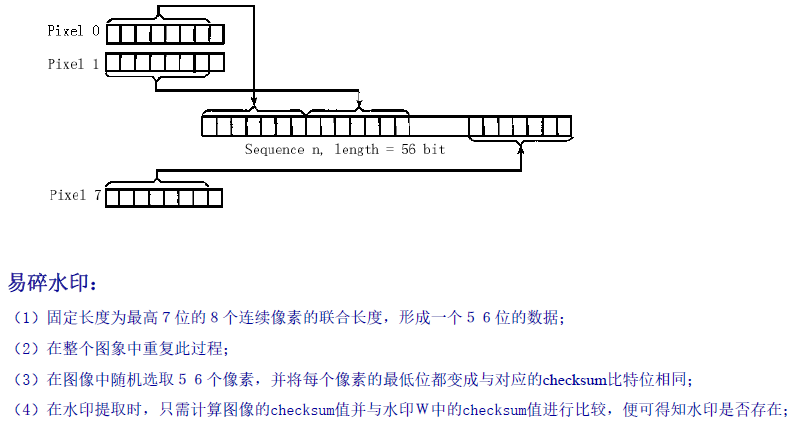
Checksum算法
频域水印算法
通过修改频域空间的系数实现水印嵌入
- 离散傅里叶变换(DFT)
- 离散余弦变换(DCT)
- 离散小波变换(DWT)
优点:鲁棒性好
缺点:复杂度高
附录
DES算法相关表
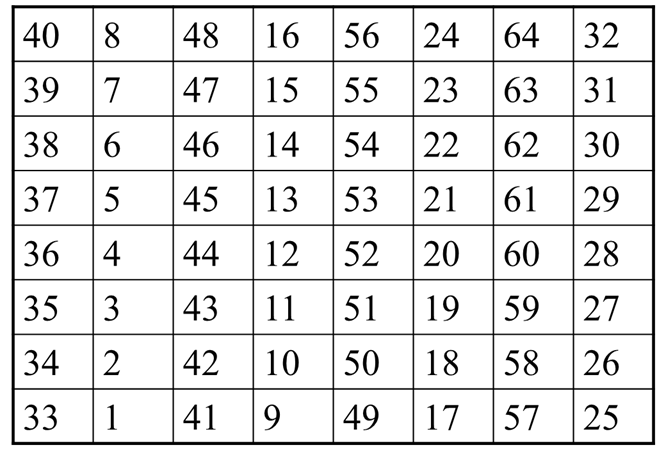
初始置换IP (对明文输入进行次序打乱)

初始置换的逆置换IP-1
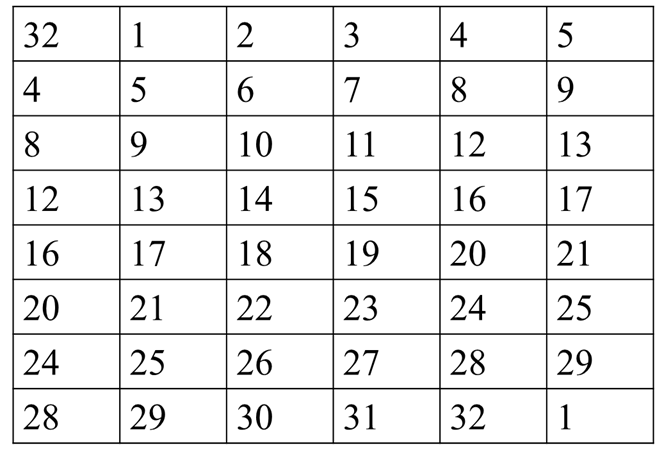
扩展置换E (32-bit到48-bit)
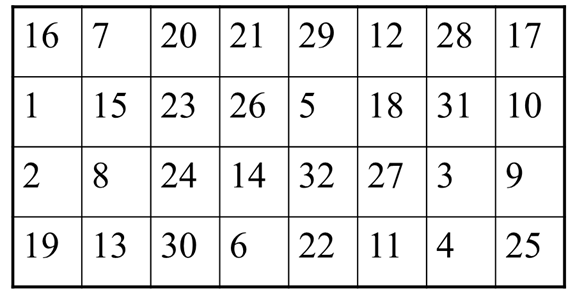
置换函数P
PC1

PC2

S-box 例子

AES算法相关表
字节替换表